problem solving | Racquel Sanderson

Tag Archives: problem solving

April 21, 2025 · 11:08 am

Area/Geometry Problem

This problem is from The Geometry Forum Problem of the Week June 1996

In triangle ABC, AC=18 and D is the point on AC for which AD=5. Perpendiculars drawn from D to AB and CB have lengths of 4 and 5 respectively. What is the area of triangle ABC?

I put together a diagram (in Geogebra)

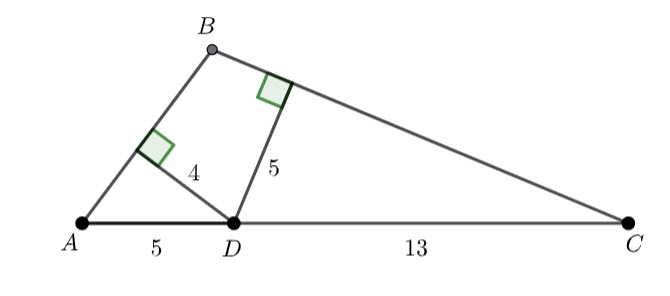
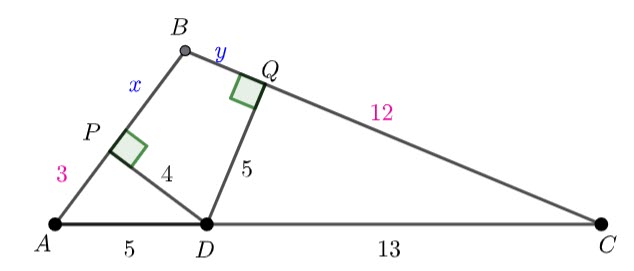
Add points P and Q

Triangle APD and triangle DQC are right angled. Using pythagoras, $AP=3$ and $QC=12$

$BQDP$ is a cyclic quadrilateral and $BD$ is the diameter. I am not sure if this is useful, but it is good to notice.

$\begin{equation*}sin(A+B+C)=sin(180)=0\end{equation}$

$\begin{equation*}sin((A+C)+B)=sin(A+C)cosB+sinBcos(A+C)=0\end{equation}$

$\begin{equation*}cosB(sinAcosC+sinCcosA)+sinB(cosAcosC-sinAsinC)=0\end{equation}$

$\begin{equation*}cosB(\frac{4}{5}\times\frac{12}{13}+\frac{5}{13}\times\frac{3}{5})+sinB(\frac{3}{5}\times\frac{12}{13}-\frac{4}{5}\times\frac{5}{13})=0\end{equation}$

$\begin{equation*}cosB(\frac{48}{65}+\frac{15}{65})+sinB(\frac{36}{65}-\frac{20}{65})=0\end{equation}$

$\begin{equation*}\frac{63}{65}cosB+\frac{16}{65}sinB=0\end{equation}$

$\begin{equation*}63cosB+16sinB=0\end{equation}$

$\begin{equation*}63+16tanB=0\end{equation}$

$\begin{equation*}tanB=\frac{-63}{16}\end{equation}$

If $tanB=\frac{-63}{16}$ then $sinB=\frac{63}{65}$

Now,

$\begin{equation*}\frac{y+12}{sinA}=\frac{18}{sinB}\end{equation}$

$\begin{equation*}y+12=\frac{4}{5}(18)\frac{65}{63}\end{equation}$

$\begin{equation*}y+12=\frac{104}{7}\end{equation}$

Hence the Area is

$\begin{equation*}A=\frac{1}{2}(18)(\frac{104}{7})sinC\end{equation}$

$\begin{equation*}A=\frac{1}{2}(18)(\frac{104}{7})\frac{5}{13}\end{equation}$

$\begin{equation*}A=\frac{360}{7}=51.43\end{equation}$

Puzzle Page 1

If $\frac{a+b+2c}{a+b-c}=\frac{31}{15}$ , what does $\frac{a+b}{c}$ equal?

$\begin{equation*}15(a+n+2c)=31(a+b-c)\end{equation}$

$\begin{equation*}15a+15b+30c=31a+31b-31c)\end{equation}$

$\begin{equation*}61c=16a+16b)\end{equation}$

$\begin{equation*}\frac{61}{16}=\frac{a+b}{c}\end{equation}$

Two positive numbers are such that their difference, their sum, and their product are in the ratio $2:5:21$ . What is the smaller of the two numbers?

Let $x$ and $y$ be the two numbers. Then

(1) $\begin{equation*}x-y=2k\end{equation*}$

(2) $\begin{equation*}x+y=5k\end{equation*}$

(3) $\begin{equation*}xy=21k\end{equation*}$

Add equation $1$ and $2$ together to eliminate the $y$

$\begin{equation*}2x=7k\end{equation}$

(4) $\begin{equation*}x=\frac{7k}{2}\end{equation*}$

From $2$ $=5k-x$ , substitute for $y$ into equation $3$ .

(5) $\begin{equation*}x(5k-x)=21k\end{equation*}$

Substitute $x=\frac{7k}{2}$ into equation $5$ .

$\begin{equation*}\frac{7k}{2}(5k-\frac{7k}{2})=21k\end{equation}$

$\begin{equation*}\frac{35k^2}{2}-\frac{49k^2}{4}=21k\end{equation}$

$\begin{equation*}\frac{70k^2}{4}-\frac{49k^2}{4}=\frac{84k}{4}\end{equation}$

$\begin{equation*}21k^2-84k=0\end{equation}$

$\begin{equation*}21k(k-4)=0\end{equation}$

Hence, $k=0$ or $k=4$ .

When $k=4$ , $x=\frac{7\times 4}{2}=14$ and $y=5\times 4-14=6$

Therefore the smaller number is $6$ .

Tag Archives: problem solving

Area/Geometry Problem

Puzzle Page 1

Recent Posts

Categories

Archives