Tag Archives: Polynomials

September 19, 2024 · 9:43 am

Solving Cubic Functions

I have been thinking about cubics a bit lately because some of my students are solving and then sketching cubics. Plus I am reading An Imaginary Tale by Paul Nahin, which talks about solving cubics and complex numbers.

Cubics must have at least one real root. If one of the roots is a rational number, then we can use the Factor and Remainder Theorem.

For example,

Solve 2x^3-3x^2-3x+2=0

We know the root(s) must be a factor of 2\times3=6.
I always start with 1 or -1
2(1)^3-3(1)^2-3(1)+2=2-3-3+2=-2 \therefore x\neq=1
Try -1
2(-1)^3-3(-1)^2-3(-1)+2=-2-3+3+2=0 \therefore x=-1 and (x+1) is a factor.
Then we can do polynomial long division.

Now we know that 2x^3-3x^2-3x+2=(x+1)(2x^2-5x+2)
And we can factorise the quadratic (or using the quadratic equation formula)
2x^2-5x+2=2x^2-4x-x+2
=2x(x-2)-1(x-2)
=(2x-1)(x-2)
\therefore x=-1, \frac{1}{2}, 2

But what if it is not factorisable?

For example,

Solve 2x^3+5x^2-2x+4=0

How many roots does this equation have?

We could find the derivative and find out how many stationary points the function has.

f'(x)=6x^2+10x-2

This is a quadratic function. Find the discriminant to determine the number of roots.

\Delta=b^2-4ac=100-4(6)(-2)=148

As \Delta>0, there are two stationary points, which means we could have 1, 2 (one root is repeated) or three roots, depending on if the function crosses the x-axis between stationary points. So not much use.

We could try the discriminant of a cubic.

\Delta=18abcd-4b^3d+b^2c^2-4ac^2-27a^2d^2

\Delta=18(2)(5)(-2)(4)-4(5^3)(4)+(5^2)(-2)^2-4(2)(-2)^2-27(2)^2(4)^2=-5100

The discriminant is negative so there is one real root.

From my reading, we need to turn the cubic into a depressed cubic (cubics of the form x^3+px+q=0).

We can do this by using a change of variable.

Let x=t-\frac{5}{6}
2(x^3+\frac{5}{2}x^2-x+2)=0
\therefore x^3+\frac{5}{2}x^2-x+2=0
Substitute t-\frac{5}{6} into the cubic.
(t-\frac{5}{6})^3+\frac{5}{2}(t-\frac{5}{6})^2-(t-\frac{5}{6})+2
(t^3-3(\frac{5}{6})t^2+3(\frac{5}{6})^2t-(\frac{5}{6})^3+\frac{5}{2}(t^2-2(\frac{5}{6})t+(\frac{5}{6})^2)-t+\frac{5}{6}+2
t^3-\frac{5}{2}t^2+\frac{25}{12}t-\frac{125}{216}+\frac{5}{2}t^2-\frac{25}{6}t+\frac{125}{72}-t+\frac{5}{6}+2
t^3-\frac{37}{12}t+\frac{431}{108}

We can then use Cardano’s formula

x=\sqrt[3]{-\frac{q}{2}+\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(-\frac{q}{2})^2+(\frac{p}{3})^3}}

p=-\frac{37}{12} and q=\frac{431}{108}
\frac{p}{3}=\frac{-37}{36}
\frac{q}{2}=\frac{431}{216}
(\frac{431}{216})^2+(\frac{-37}{36})^3=\frac{139}{48}
t=\sqrt[3]{\frac{-431}{216}+\sqrt{\frac{139}{48}}}+\sqrt[3]{\frac{-431}{216}-\sqrt{\frac{139}{48}}}
t=-2.21095...
\therefore x=-2.21095...-\frac{5}{6}=-3.044

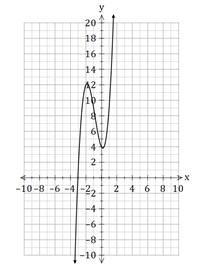
We can see from the sketch below that there is only one solution and it is about -3.

1 Comment

Filed under Cubics, Factorising, Polynomials, Solving

Tagged as , , , , ,

September 14, 2024 · 9:45 am

Sum and Product of the Roots of Polynomials

There is a relationship between the sum and product of the roots of a polynomial and the co-efficient of the polynomial.

Let’s start with a quadratic.

The general form for a quadratic (polynomial of degree 2) is

y=ax^2+bx+c

Use the quadratic equation formula to find the roots

x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}

Hence the roots are

x_1=\frac{-b+\sqrt{b^2-4ac}}{2a} and x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}

Sum of the roots:

\frac{-b+\sqrt{b^2-4ac}}{2a}+\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{-2b}{2a}=\frac{-b}{a}

Product of the roots:

\frac{-b+\sqrt{b^2-4ac}}{2a}\times\frac{-b-\sqrt{b^2-4ac}}{2a}

\frac{b^2}{4a^2}-\frac{b^2-4ac}{4a^2}

\frac{4ac}{4a^2}

\frac{a}{c}

Worked Example
The equation 4x^2+bx+c=0 has two distinct roots. The product of the roots is \frac{3}{4} and the sum is 2. Find b and c.
\frac{-b}{a}=2
a=4
\frac{-b}{4}=2
b=-8

\frac{c}{a}=\frac{3}{4}
\frac{c}{4}=\frac{3}{3}
c=3
The equations is 4x^2-8x+3

Solve the equation to prove the roots do in fact sum to 2 and multiply to \frac{3}{4}
4x^2-8x+3
4x^2-6x-2x+3
2x(2x-3)-1(2x-3)
(2x-1)(2x-3)
x_1=\frac{1}{2} and x_2=\frac{3}{2}
\frac{1}{2}+\frac{3}{2}=2 and \frac{1}{2}\times\frac{3}{2}=\frac{3}{4}

Let’s move to a cubic function.

The general equation is f(x)=ax^3+bx^2+cx+d

Let’s say the roots of this cubic are \alpha, \beta, \gamma

Then ax^3+bx^2+cx+d=a(x-\alpha)(x-\beta)(x-\gamma)

=a(x^2-\beta x - \alpha x+\alpha\beta)(x-\gamma)

=a(x^2-(\alpha+\beta)x+\alpha\beta)(x-\gamma)

=a(x^3-\gamma x^2-x^2(\alpha+\beta)+\gamma(\alpha+\beta)x-\alpha\beta\gamma)

=a(x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\alpha\gamma+\beta\gamma)x-\alpha\beta\gamma)

The sum of the roots

\alpha+\beta+\gamma=\frac{-b}{a}

The product of the roots

\alpha\beta\gamma=\frac{-d}{a}

Also, it can be handy to know

\alpha\beta+\alpha\gamma+\beta\gamma=\frac{c}{a}

Worked example
f(x)=x^3-6x^2+4x+12, the roots are \alpha, \beta and \gamma
Find
(a) \alpha+\beta+\gamma
(b) \alpha^2+\beta^2+\gamma^2
(c) \frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}

(a) \alpha+\beta+\gamma=\frac{-b}{a}
\alpha+\beta+\gamma=\frac{6}{1}
\alpha+\beta+\gamma=6

(b)\alpha^2+\beta^2+\gamma^2=(\alpha+\beta+\gamma)^2-2\alpha\beta-2\alpha\gamma-2\beta\gamma
=6^2-2(4)
=28

(c)\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}=\frac{\beta\gamma}{\alpha\beta\gamma}+\frac{\alpha\gamma}{\alpha\beta\gamma}+\frac{\alpha\beta}{\alpha\beta\gamma}
=\frac{\beta\gamma+\alpha\gamma+\alpha\beta}{\alpha\beta\gamma}
=\frac{4}{-13}
=\frac{-1}{3}

We can extend the method we used for finding the sum and product of the roots of cubic to polynomials of greater degree.

If the four roots of a quartic are \alpha, \beta, \gamma and \delta, and the general equation is ax^4+bx^3+cx^2+dx+e, then

\alpha+\beta+\gamma+\delta=\frac{-b}{a}

\alpha\beta+\alpha\gamma+\alpha\delta+\beta\gamma+\beta\delta+\gamma\delta=\frac{c}{a}

\alpha\beta\gamma+\alpha\beta\delta+\alpha\gamma\delta+\beta\gamma\delta=\frac{-d}{a}

\alpha\beta\gamma\delta=\frac{e}{a}

Worked Example (just one more)
The roots of the cubic equation x^3-4x^2-3x-2 are \alpha, \beta and \gamma. Find the cubic equation whose roots are \alpha+\beta, \alpha+\gamma, and \beta+\gamma

\alpha+\beta+\gamma=4
\alpha\beta+\alpha\gamma+\beta\gamma=-3
\alpha\beta\gamma=2

\frac{-b}{a}=\alpha+\beta+\alpha+\gamma+\beta+\gamma
\frac{-b}{a}=2(\alpha+\beta+\gamma
\frac{-b}{a}=2(4)
\frac{-b}{a}=8

\frac{c}{a}=(\alpha+\beta)(\alpha+\gamma)+(\alpha+\beta)(\beta+\gamma)+(\alpha+\gamma)(\beta+\gamma)
=\alpha^2+\alpha\gamma+\beta\gamma+\gamma^2+\alpha\beta+\alpha\gamma+\beta^2+\beta\gamma+\alpha\beta+\alpha\gamma+\gamma\beta+\gamma^2
=\alpha^2+\beta^2+\gamma^2+3\alpha\gamma+3\beta\gamma+3\alpha\beta
=(\alpha+\beta+\gamma)^2-2\alpha\gamma-2\beta\gamma-2\alpha\beta+3\alpha\gamma+3\beta\gamma+3\alpha\beta
=(\alpha+\beta+\gamma)^2+\alpha\gamma+\alpha\beta+\beta\gamma
=4^2-3
\frac{c}{a}=13

\frac{-d}{a}=(\alpha+\beta)(\alpha+\gamma)(\beta+\gamma)
=(\alpha^2+\alpha\gamma+\beta\alpha+\beta\gamma)(\beta+\gamma)
=\alpha^2\beta+\alpha^2\gamma+\alpha\gamma\beta+\alpha\gamma^2+\beta^2\alpha+\beta\alpha\gamma+\beta^2\gamma+\beta\gamma^2
=2\alpha\beta\gamma+\alpha^2\beta+\beta^2\alpha+\alpha^2\gamma+\gamma^2\alpha+\beta^2\gamma+\gamma^2\beta
=2(2)+\alpha\beta(\alpha+\beta)+\alpha\gamma(\alpha+\gamma)+\beta\gamma(\beta+\gamma)
=-24+\alpha\beta(\alpha+\beta+\gamma)-\alpha\beta\gamma+\alpha\gamma(\alpha+\gamma+\beta)-\alpha\beta\gamma+\beta\gamma(\beta+\gamma+\alpha)-\beta\gamma\alpha
=4+(\alpha+\beta+\gamma)(\alpha\beta+\alpha\gamma+\beta\gamma)-3(2)
=-2+(4)(-3)
\frac{-d}{a}=-14

If a=1 then b=-8, c=13 and d=14
The cubic is x^3-8x^2+13x+14

1 Comment

Filed under Polynomials, Sum and Product of Roots

Tagged as , , ,

July 16, 2024 · 7:35 am

Australian Mathematics Competition – Polynomial Question

I came across this question from the 2010 Senior Australian Mathematics Competition:

A polynomial f is given. All we know about it is that all its coefficients are non-negative integers, f(1)=6 and f(7)=3438. What is the value of f(3)

Australian Mathematics Competition 2006-2012

I thought ‘excellent, a somewhat hard polynomial question for my students’ and then I tried it. Now I know why only 1% of students got it correct.

As we don’t know the order of the polynomial, let

f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0

We know all of the coefficients are greater than or equal to zero. We also know

f(1)=a_n+a_{n-1}+...+a+a_0=6

Which means that all of the coefficients are between zero and six

0\le{a_n}\le{6}

We have also been given f(7)

f(7)=7^na_n+7^{n-1}a_{n-1}+ ... +7a+1=3438

As all of the coefficients are between zero and six, this is 3438 written in base 7.

Let’s calculate a few powers of 7

Powers of 7
7^01
7^17
7^249
7^3343
7^42401
7^516807
As numbersAs Powers of 7
3438=1\times2401+10373438=1\times7^4+1037
1037=3\times343+81037=3\times7^3+8
8=1\times7+18=1\times7^1+1
1=1\times11=1\times7^0

Hence 3438 written in base 7 is 13011

Therefore f(x)=x^4+3x^3+x+1

f(3)=3^4+3\times3^3+3+1

f(3)=81+81+4

f(3)=166

I really like this question. I think it could work well as a class extension activity with a bit of scaffolding.

Leave a Comment

Filed under Number Bases, Polynomials

Tagged as , ,