Tag Archives: intersection of circles and lines

May 9, 2024 · 6:08 am

Intersections of Lines and Circles

The three possibilities: no intersection, one point of intersection, or two points of intersection

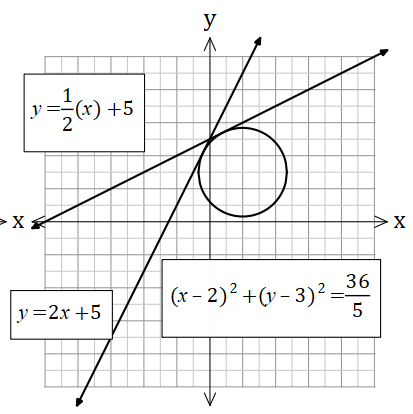
Once my students have studied circle and quadratic equations, I like to introduce lines intersecting with circles. It tests their quadratic equation solving skills, and if they can use the discriminant.

Example 1

Calculate the point(s) of intersection of

$3x+2y-6=0\ \textnormal{and}\ (x+4)^2+(y+2)^2=9$

Rearrange the line equation

$y=\frac{6-3x}{2}$

$y=3-\frac{3x}{2}$

Substitute for y into the circle equation

$(x+4)^2+(3-\frac{3x}{2}+2)^2=9$

$(x+4)^2+(5-\frac{3x}{2})^2=9$

$x^2+8x+16+25-15x+\frac{9x^2}{4}-9=0$

$\frac{13x^2}{4}-7x+32=0$

$13x^2-28x+128=0$

At this point I like to check the discrimnant

$\Delta=b^2-4ac$

$\Delta=(-28)^2-4\times13\times128$

$\Delta=-5872$

As the discriminate is less than zero, there are no points of intersection.

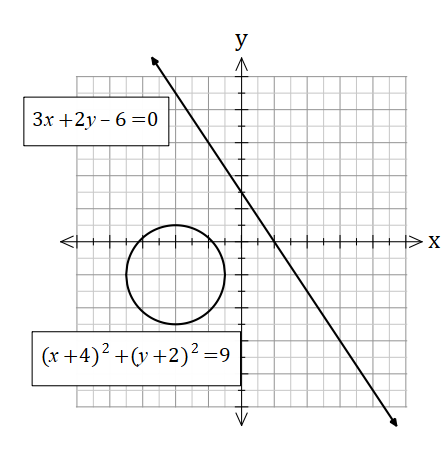
Example 2

Calculate the point(s) of intersection of

$y=2x+1\ \textnormal{and}\ (x+5)^2+(y+3)^2=16$

$(x+5)^2+(2x+1+3)^2=16$

$(x+5)^2+(2x+4)^2=16$

$x^2+10x+25+4x^2+16x+16-16=0$

$5x^2+26x+25=0$

Check the discriminant

$\Delta=26^2-4\times5\times25$

$\Delta=176$

Therefore there are two points of intersection

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

$x=\frac{-26\pm\sqrt{176}}{10}$

$x=\frac{-26\pm4\sqrt{11}}{10}$

$x=\frac{-13\pm2\sqrt{11}}{5}$

Substitute x into y

$y=2(\frac{-13\pm2\sqrt{11}}{5})+1$

$\textnormal{The two points are}\ (\frac{-13+2\sqrt{11}}{5},\frac{-21+4\sqrt{11}}{5})$

$\textnormal{and}\ (\frac{-13-2\sqrt{11}}{5},\frac{-21-4\sqrt{11}}{5})$

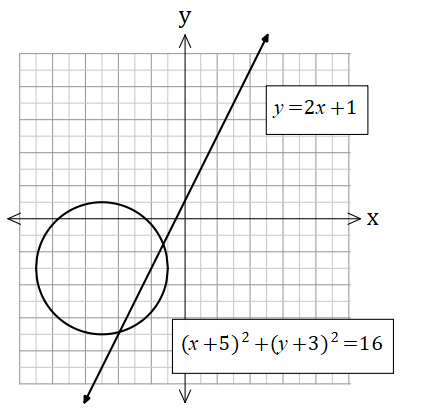
Example 3

Find the value of k so that the line and the circle intersect at one point (i.e. the line is a tangent to the circle)

$-kx+y-5=0\ \textnormal{and}\ (x-2)^2+(y-3)^2=\frac{36}{5}$

$y=kx+5$

$(x-2)^2+(kx+5-3)^2=\frac{36}{5}$

$(x-2)^2+(kx+2)^2=\frac{36}{5}$

$x^2-4x+4+k^2x^2+4kx+4-\frac{36}{5}=0$

$(1+k^2)x^2+(4k-4)x+\frac{4}{5}=0$

Find the discriminant (remember for one solution we want the discriminant to be zero)

$\Delta=b^2-4ac$

$\Delta=(4k-4)^2-4\times(1+k^2)\times\frac{4}{5}$

$\Delta=16k^2-32k+16-\frac{16}{5}-\frac{16k^2}{5}$

$0=16k^2-32k+16-\frac{16}{5}-\frac{16k^2}{5} \[0=80k^2-160k+80-16-16k^2$

$0=64k^2-160k+64$

$0=32(2k^2-5k+2)$

$0=2k^2-5k+2$

$0=2k^2-4k-k+2$

$0=2k(k-2)-1(k-2)$

$0=(2k-1)(k-2)$

$k=\frac{1}{2}\ \textnormal{and}\ k=2$

Leave a Comment

Filed under Circles and Quadratics, Quadratics

Tagged as discriminant, intersection of circles and lines, quadratics