I think this one is doing the rounds, I first saw it here.
![]()
![]() is the obvious answer,
is the obvious answer, ![]() , but are there more answers?
, but are there more answers?
This was my approach
![]()
![]()
![]()
![]()
A quadratic equation.
Hence,
![]()
I then used my calculator
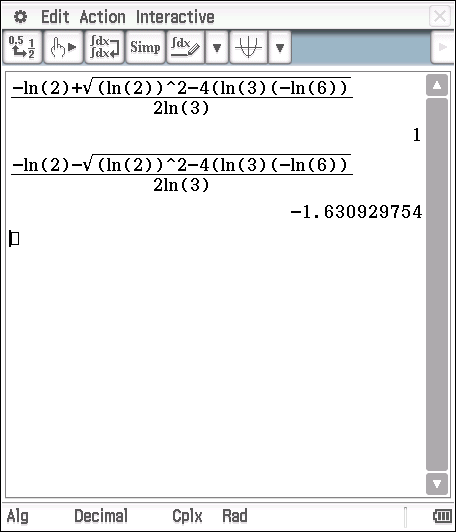
Hence ![]() 0r
0r ![]()
I think this one is doing the rounds, I first saw it here.
![]()
![]() is the obvious answer,
is the obvious answer, ![]() , but are there more answers?
, but are there more answers?
This was my approach
![]()
![]()
![]()
![]()
A quadratic equation.
Hence,
![]()
I then used my calculator

Hence ![]() 0r
0r ![]()
Filed under Algebra, Index Laws, Interesting Mathematics, Quadratics, Solving