Two circles have the same centre ![]() . The smaller circle has a radius of
. The smaller circle has a radius of ![]() cm, while the larger has a radius of
cm, while the larger has a radius of ![]() cm. The circles enclose a region
cm. The circles enclose a region ![]() , which is subtended by angle of
, which is subtended by angle of ![]() at
at ![]() , as shaded.
, as shaded.
The area of ![]() is
is ![]() cm2, where
cm2, where ![]() is a constant and
is a constant and ![]()
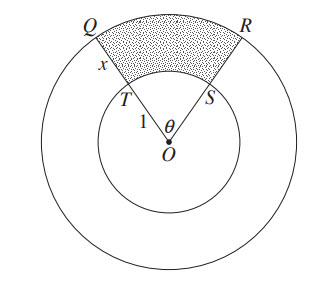
Let ![]() cm be the perimeter of
cm be the perimeter of ![]()
(a) By finding expressions for the area and perimeter of ![]() show that
show that ![]()
(b) Show that if the perimeter is minimised, then ![]() must be less than
must be less than ![]() .
.
| (a) I like it when the first part requires the student to show something and the second part has them use it (that way they can still do the second part even if they couldn’t do the first part). (b) Both Substitute Now Hence and |
