Tag Archives: geometry

September 29, 2024 · 10:18 am

Intersecting Circles

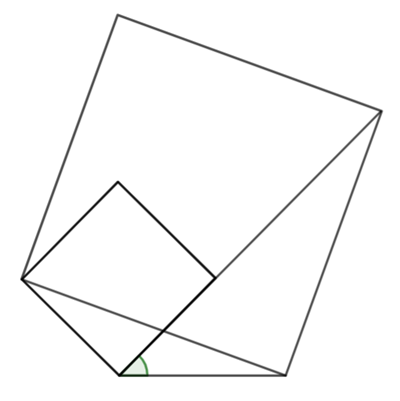
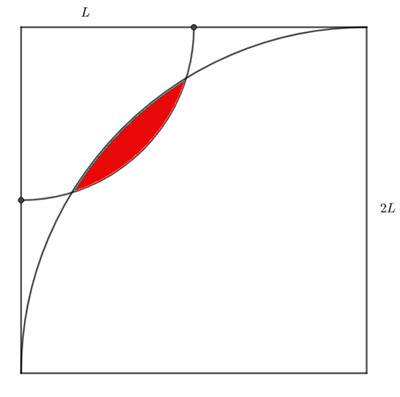
Two circles of radius $L$ and $2L$ intersect as shown. What is the area of the shaded region?

From Professor Povey’s Perplexing Problems

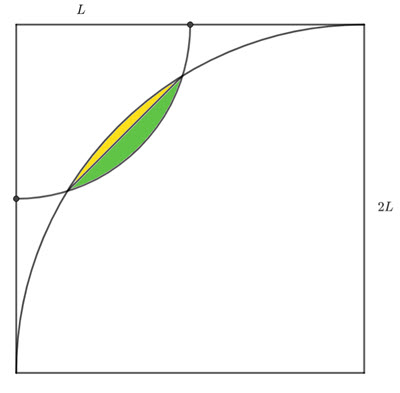
My plan is to find the sum of the area of the two segments (see below).

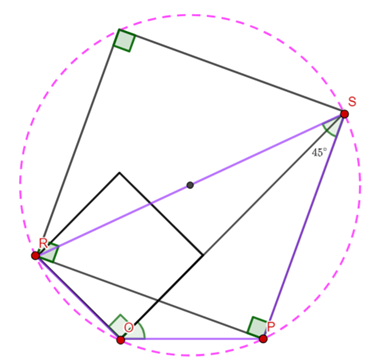
Construct triangles

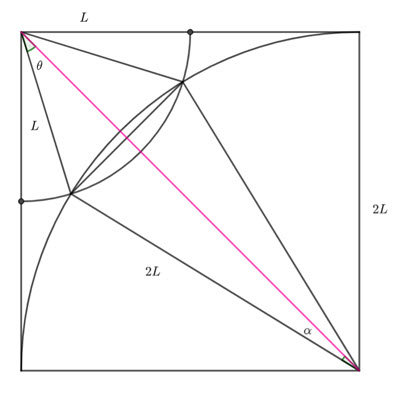
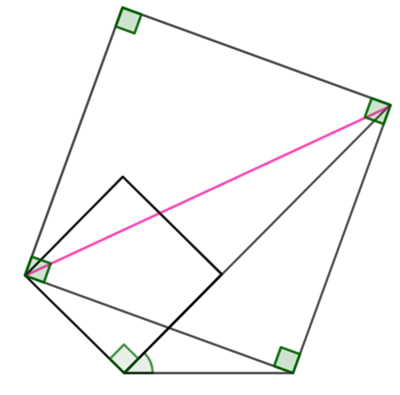
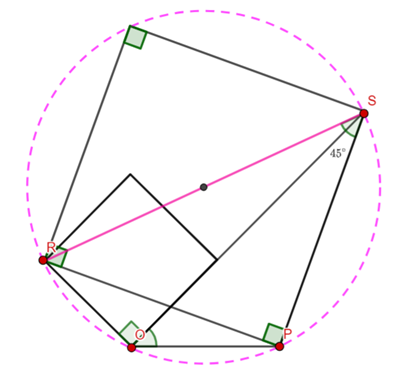
The diagonal of the square (the pink line above) has length

$=\sqrt{(2L)^2+(2L)^2}=\sqrt{8L^2}=2\sqrt{2}L$

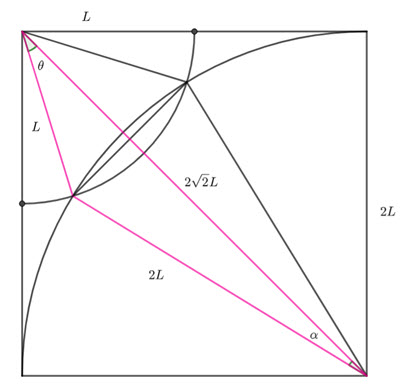
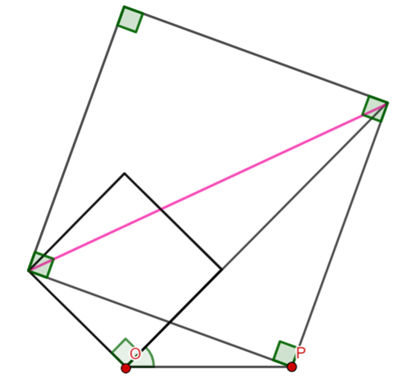
From the pink triangle in the above diagram, I am going to find the angles using the cosine rule.

$cos\theta=\frac{L^2+(2\sqrt{2}L)^2-(2L)^2}{2(L)(2\sqrt{2}L)}$

$cos\theta=\frac{5L^2}{4\sqrt{2}L^2}$

$cos\theta=\frac{5}{4\sqrt{2}}$

$\theta=0.487$

$cos\alpha=\frac{(2L)^2+(2\sqrt{2}L)^2-L^2}{(2\sqrt{2}L)(2L)}$

$cos\alpha=\frac{11L^2}{8\sqrt{2}L^2}$

$cos\alpha=\frac{11}{8\sqrt{2}}$

$\alpha=0.236$

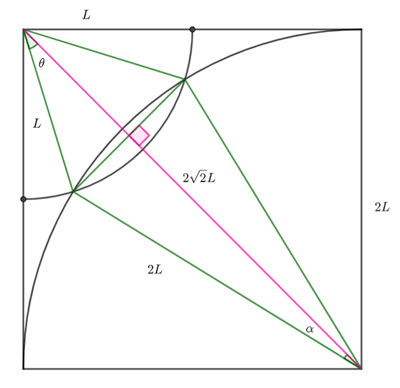
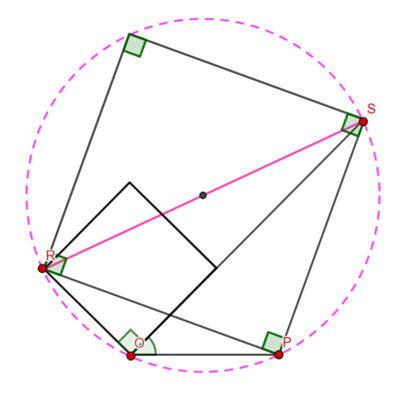
The green quadrilateral is a kite, which means the diagonals are perpendicular.

This means the segment angles are $2\theta$ and $2\alpha$ (because the triangles are isosceles and the diagonal is perpendicular to the base of the triangles).

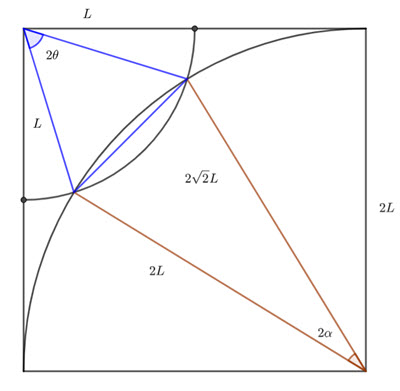
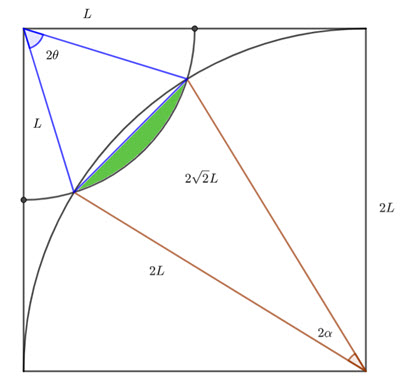
Area of green segment

$A=\frac{1}{2}r^2(\theta-sin\theta)$

$A=\frac{1}{2}L^2(0.9734-sin(0.9734))=0.0733L^2$

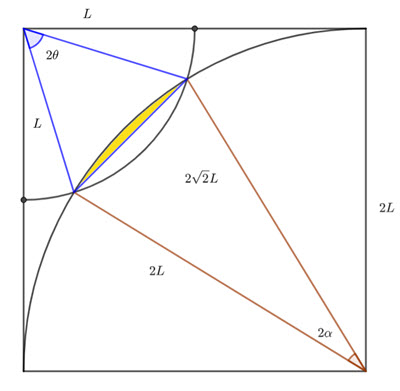
Area of yellow segment

$A=\frac{1}{2}4L^2(0.4721-sin(0.4721))=0.0035$

Total Area = $0.0733L^2+0.0035L^2=0.108L^2$

Leave a Comment

Filed under Finding an area, Geometry, Professor Povey

Tagged as finding an unknown shaded area, geometry, professor povey

September 7, 2024 · 9:31 am

Geometry Problem

This problem is from Geometry Snacks by Ed Southall and Vincent Pantaloni – it’s a great book.

Two squares are constructed such that three vertices are collinear as shown. Find the value of the marked angle.

I started by marking in the right angles. And I added the diagonal of the larger square (pink line).

Because there are right angles at $O$ and $P$ , we know there is a circle, which has the diagonal of the square as its diameter (see second image below).

$\angle{RSP}$ is $45^{\circ}$ (Angle between the diagonal and side of a square)

$PORS$ is a cyclic quadrilateral.

In cyclic quadrilaterals opposite angles are supplementary.

Hence, $\angle{ROP}=180^{\circ}-45^{\circ}=135^{\circ}$

As $\angle{ROS}=90^{\circ}$ , $\angle{SOP}$ must be $45^{\circ}$

Leave a Comment

Filed under Finding an angle, Geometry

Tagged as circle geometry, finding an angle, geometry, squares