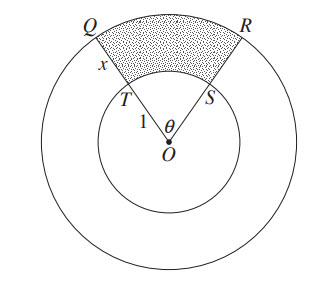
In the last post we looked at two trig limits:
(1) ![]()
(2) ![]()
We are going to use these two limits to differentiate sine and cosine functions from first principals.
![]()
![]()
Use the trig identity
![]()
![]()
![]()
![]()
![]()
Evaluate the limits
![]()
Hence, ![]() .
.
Now we are going to do the same for ![]() .
.
![]()
Use the trigonometric identity
![]()
![]()
![]()
![]()
Evaluate the limits
![]()
Hence ![]()