bisecting an angle | Racquel Sanderson

Points $A$ and $B$ are defined by the position vectors $\mathbf{a}=3\mathbf{i}+4\mathbf{j}$ and $\mathbf{b}=12\mathbf{i}+5\mathbf{j}$ .

Find a vector that bisects $\angle{AOB}$ .

If we think about how we add vectors using the parallelogram rule

Finding the resultant vector using the parallelogram rule

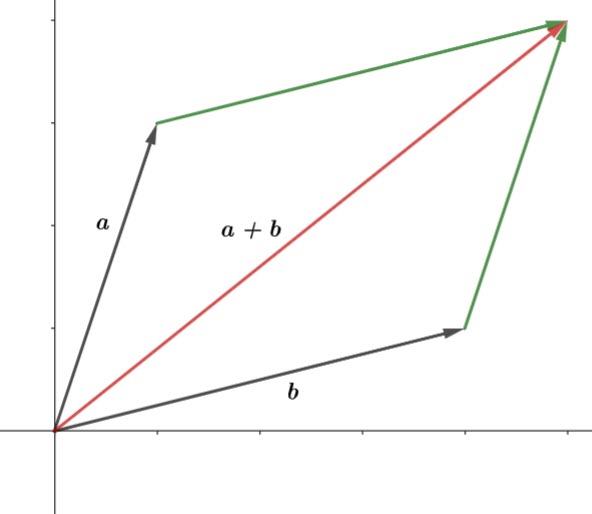
we can take advantage of the geometric properties of parallelograms (or of a rhombus).

If $\mathbf{a}$ and $\mathbf{b}$ are unit vectors, then the parallelogram is a rhombus, and the diagonal (i.e the resultant) bisects the angle.

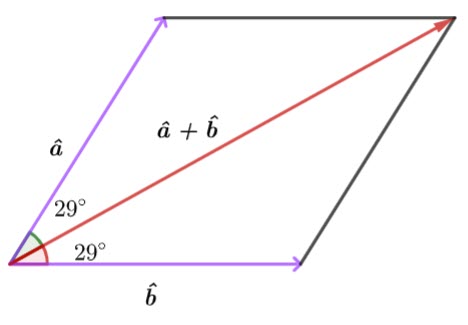
We need to find the sum of the unit vectors.

$|\mathbf{a}|=\sqrt{3^2+4^2}=5$

$\therefore \hat{\mathbf{a}}=\frac{3}{5}\mathbf{i}+\frac{4}{5}\mathbf{j}$

$|\mathbf{b}|=\sqrt{12^2+5^2}=13$

$\therefore \hat{\mathbf{b}}=\frac{12}{13}\mathbf{i}+\frac{5}{13}\mathbf{j}$

The vector that bisects $\angle{AOB}$ is

$\frac{3}{5}\mathbf{i}+\frac{4}{5}\mathbf{j}+\frac{12}{13}\mathbf{i}+\frac{5}{13}\mathbf{j}=\frac{99}{65}\mathbf{i}+\frac{64}{65}\mathbf{j}$

Tag Archives: bisecting an angle

Using a Vector Method to Find an Angle Bisector

Recent Posts

Categories

Archives