A circle has equation
(a) Find the centre and radius of the circle.
Pointsand
lie on the circle such that the origin is the midpoint of
.
(b) Show thathas a length of 12.
(a)We need to put the circle equation into completed square form
![]()
![]()
The centre is ![]() and the radius is
and the radius is ![]() .
.
(b)Draw a diagram
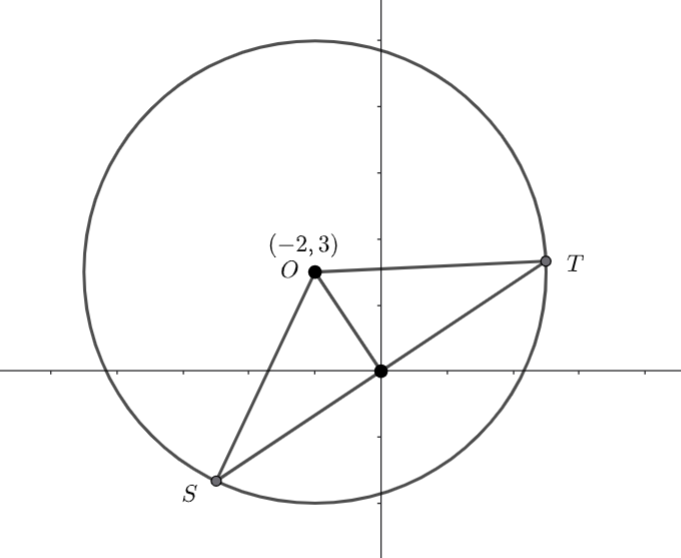
We know ![]() and
and ![]() are radii of the circle. Hence
are radii of the circle. Hence ![]() is isosceles and the line segment from
is isosceles and the line segment from ![]() to the origin is perpendicular to
to the origin is perpendicular to ![]() .
.
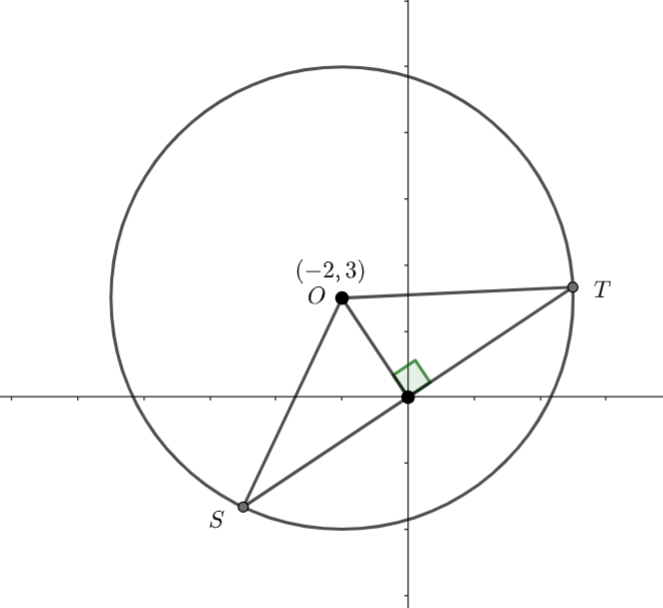
![]() and the distance from
and the distance from ![]() to the origin is
to the origin is
![]()
We can use Pythagoras to find the distance from the origin to ![]() .
.
![]()
Hence ![]()

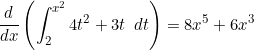
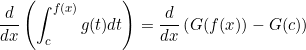











 line)
line)