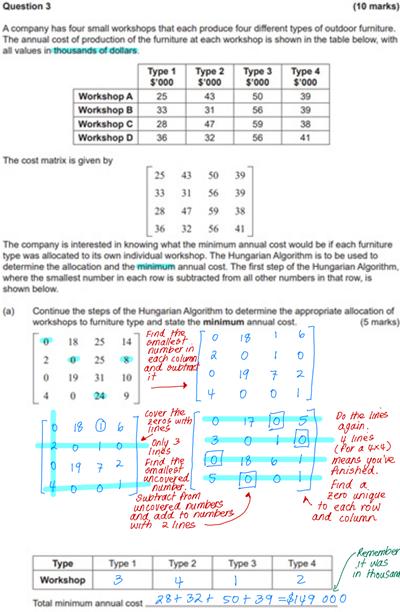
How do we go about finding the rule for a first order linear recurrence relation?
Something like
![]()
There isn’t a common difference (arithmetic sequence) or a common ratio (geometric sequence). Sometimes you can just see the rule, but an algorithm will be handy.
Let’s say our relationship is
(1) ![]()
Referring back to our sequence ![]() , we know
, we know
(2) ![]()
and
(3) ![]()
We can solve equation ![]() and
and ![]() simultaneously
simultaneously
equation ![]() equation
equation ![]()
![]()
Hence ![]()
Substitute ![]() into equation
into equation ![]()
![]()
![]()
Hence ![]()
![]()
Let’s try to generalise
If ![]() , then
, then
(4) ![]()
(5) ![]()
Equation ![]() equation
equation ![]()
![]()
![]()
Hence, ![]()
Once you know ![]() , substitute into either equation to find
, substitute into either equation to find ![]() .
.
Example
Find the recursive rule for the following
![]()
![]()
![]()
![]()
Hence ![]() and
and ![]()
It is also possible to find the rule using a Classpad (if it’s in the calculator section} by using an e-activity.