The vector projection (vector resolution or vector component) of ![]() onto a non-zero vector
onto a non-zero vector ![]() is splitting
is splitting ![]() into two vectors, one is parallel to
into two vectors, one is parallel to ![]() (the vector projection) and one perpendicular to
(the vector projection) and one perpendicular to ![]()
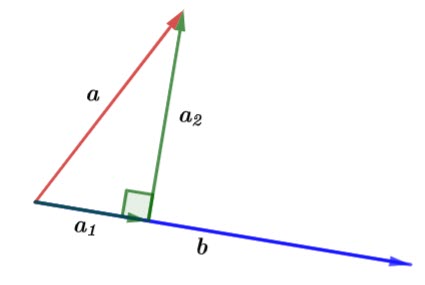
In the above diagram ![]() is the vector projection of
is the vector projection of ![]() onto
onto ![]() and
and ![]() is perpendicular to
is perpendicular to ![]() .
.
How do we find ![]() and
and ![]() ?
?
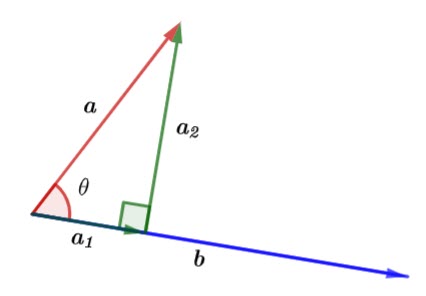
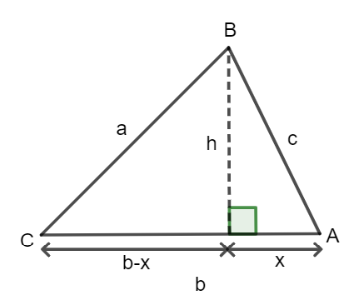
Using right trigonometry,
![]()
Remember the scalar product (dot product) of vectors is
(1) ![]()
Hence ![]()
![]()
and, ![]()
![]()
This is the scalar projection of ![]() onto
onto ![]()
To find the vector projection we need to multiply by ![]() , that is find a vector with the same magnitude as
, that is find a vector with the same magnitude as ![]() in the direction of
in the direction of ![]() .
.
The vector projection is
![]()
![]()
![]()
Now for ![]() , we know
, we know ![]()
Hence, ![]()
Example

(a) ![]()
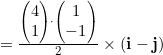
![]()
(b)![]()
(c)
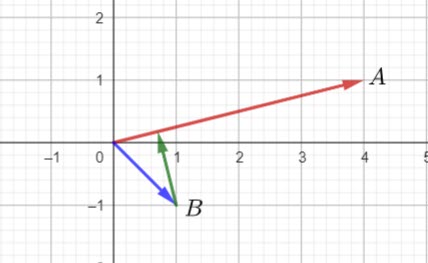
The shortest distance (green vector) is the vector component of ![]() perpendicular to
perpendicular to ![]() , i.e.
, i.e. ![]()
![]()