Solve ![]() for
for ![]()
Remember the identity
(1) ![]()
Hence
![]()
Now I have
![]()
![]()
![]() or
or ![]()
![]()
![]() for
for ![]()
![]()
![]()
Hence ![]()
Solve ![]() for
for ![]()
Remember the identity
(1) ![]()
Hence
![]()
Now I have
![]()
![]()
![]() or
or ![]()
![]()
![]() for
for ![]()
![]()
![]()
Hence ![]()
Find exactly ![]()
We must be able to find an arithmetic combination of the exact values we knew to find ![]() .
.
![]()
![]()
I re-arranged as above, so I could take advantage of ![]() and
and ![]()
| Useful identities |
![]()
![]()
![]()
![]()
![]()
![]()
Hence,
![]()
![]()
![]()
Use the quadratic equation formula
![]()
![]()
![]()
![]()
![]()
As ![]() ,
, ![]()
We are going to find a matrix to rotate a point about the origin a number of degrees (or radians).

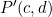

![]() and
and ![]() are equidistant from the origin. I.e.
are equidistant from the origin. I.e. ![]()
Remember, anti-clockwise angles are positive.
![]()
![]()
Use the cosine addition identity.
![]()
![]()
(1) ![]()
We will do the same for ![]()
![]()
![]()
Use the sine addition identity.
![]()
![]()
(2) ![]()
Let ![]() be the rotation matrix, then
be the rotation matrix, then
![]()
Hence ![]() must be
must be
(3) ![]()
Find the image of the line ![]() after it is rotated
after it is rotated ![]() about the origin.
about the origin.
I am going to select two points on the line and transform them.
![]()

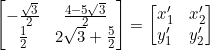
We can then find the equation of the line.
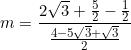
![]()
![]()
![]()

Let’s think about the sine and cosine addition and subtraction trig identities.
(1) ![]()
(2) ![]()
If we add equation ![]() and
and ![]() , we get
, we get
![]()
Hence, ![]()
If we subtract equation ![]() from equation
from equation ![]() , we get
, we get
![]()
Hence, ![]()
What about the cosine addition and subtraction idenities?
(3) ![]()
(4) ![]()
If we add equation ![]() and
and ![]() , we get
, we get
![]()
Hence, ![]()
If we subtract ![]() from
from ![]() , we get
, we get
![]()
Hence, ![]()
These are the product to sum identities.
(1) Solve ![]() for
for ![]()
Remember,
![]()
![]()
![]()
Therefore, ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence ![]()
(2)Solve ![]() for
for ![]()
![]()
Therefore, ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
Hence ![]()
Using an appropriate double angle identity, find the exact value of
The double angle identity for sine is
(1) ![]()
That means ![]() is either
is either ![]() or
or ![]() .
.
It must be ![]() as
as ![]() as there are exact values for
as there are exact values for ![]()
Hence,
![]()
![]()
![]()
![]()
![]()
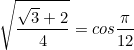
As ![]() is in the first quadrant, we don’t need to consider the negative version.
is in the first quadrant, we don’t need to consider the negative version.
![]()
Filed under Algebra, Identities, Trigonometry, Year 11 Mathematical Methods
This problem is from The Geometry Forum Problem of the Week June 1996
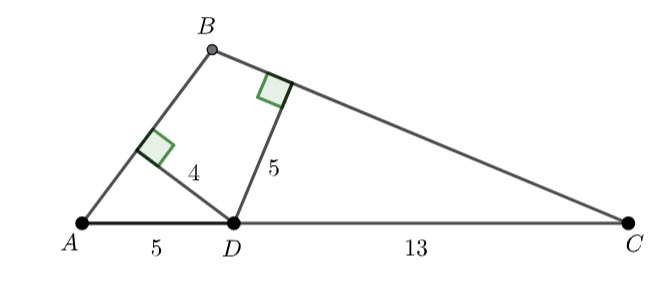
In triangle ABC, AC=18 and D is the point on AC for which AD=5. Perpendiculars drawn from D to AB and CB have lengths of 4 and 5 respectively. What is the area of triangle ABC?
I put together a diagram (in Geogebra)
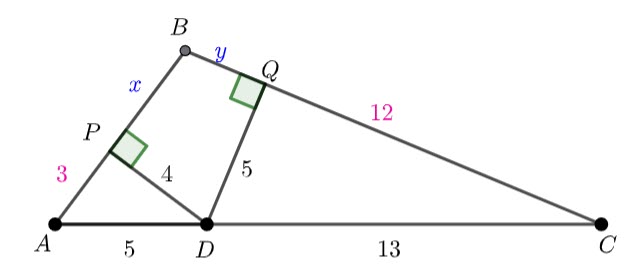
Add points P and Q

Triangle APD and triangle DQC are right angled. Using pythagoras, ![]() and
and ![]()
![]() is a cyclic quadrilateral and
is a cyclic quadrilateral and ![]() is the diameter. I am not sure if this is useful, but it is good to notice.
is the diameter. I am not sure if this is useful, but it is good to notice.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If ![]() then
then ![]()
Now,
![]()
![]()
![]()
Hence the Area is
![]()
![]()
![]()
Filed under Area, Finding an area, Geometry, Identities, Non-Right Trigonometry, Pythagoras, Trigonometry
Remember ![]() .
.
I use the quotient rule to differentiate ![]() .
.
(1) ![]()
If ![]() then from equation
then from equation ![]()
(2) ![]()
(3) ![]()
Remember the Pythagorean identity
(4) ![]()
Hence
![]()
(5) ![]()
In the last post we looked at two trig limits:
(1) ![]()
(2) ![]()
We are going to use these two limits to differentiate sine and cosine functions from first principals.
![]()
![]()
Use the trig identity
![]()
![]()
![]()
![]()
![]()
Evaluate the limits
![]()
Hence, ![]() .
.
Now we are going to do the same for ![]() .
.
![]()
Use the trigonometric identity
![]()
![]()
![]()
![]()
Evaluate the limits
![]()
Hence ![]()
Filed under Calculus, Differentiation, Identities, Trigonometry, Year 12 Mathematical Methods