I worked on this question with one of my students (I don’t know where it is from).
Mike leaves the rose bush he was examining and walks 35m in the direction S From there he walks 70m towards a rotunda. Mike is now 100m from the rose bush. Find the bearing of the rotunda from the pond. |
Let’s try to draw a diagram
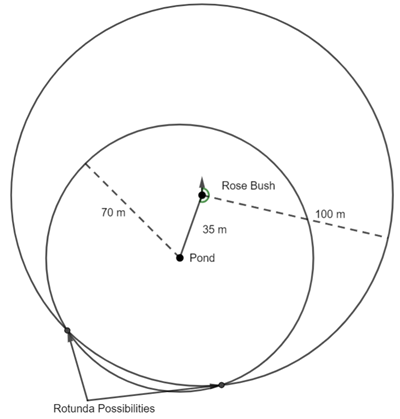
Because we don’t the direction Mike walked from the pond, I have drawn a circle with radius 70m centred at the pond.
We know Mike is now 100m from the rose bush. As we don’t know the direction, I have drawn another circle with radius 100m centred at the rose bush. Where the two circles intersect are the possible locations of the rotunda.
First Position
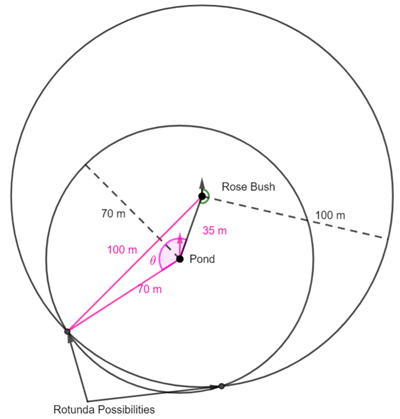
Use the cosine rule to find the angle![]()
![]()
![]()
![]()

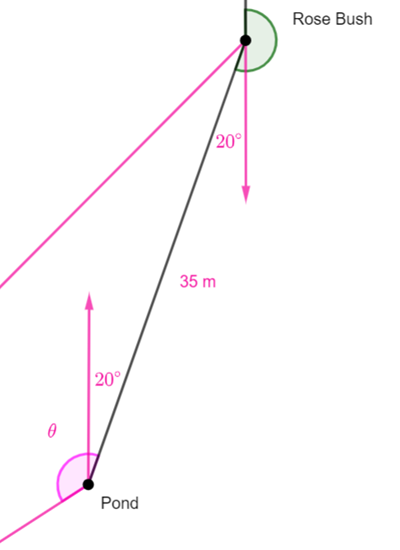
Using the fact that alternate angles in parallel lines are congruent, we can see
that the bearing from the pond to the rotunda is![]()
Second Position
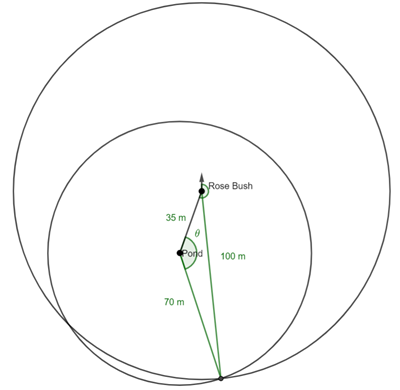
It is the same triangle, so![]()
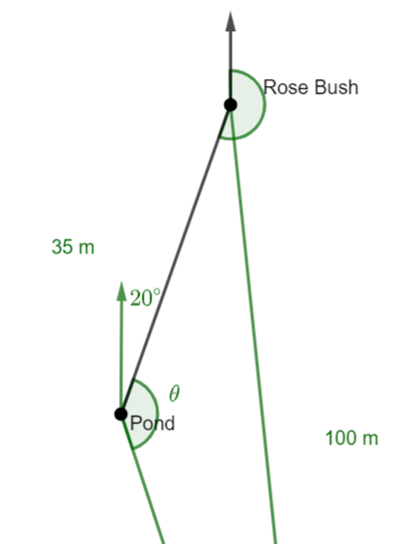
This time the bearing is![]()
Hence, the two possible bearings of the rotunda from the pond are ![]() or
or ![]() .
.
