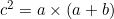This problem is from The Geometry Forum Problem of the Week June 1996
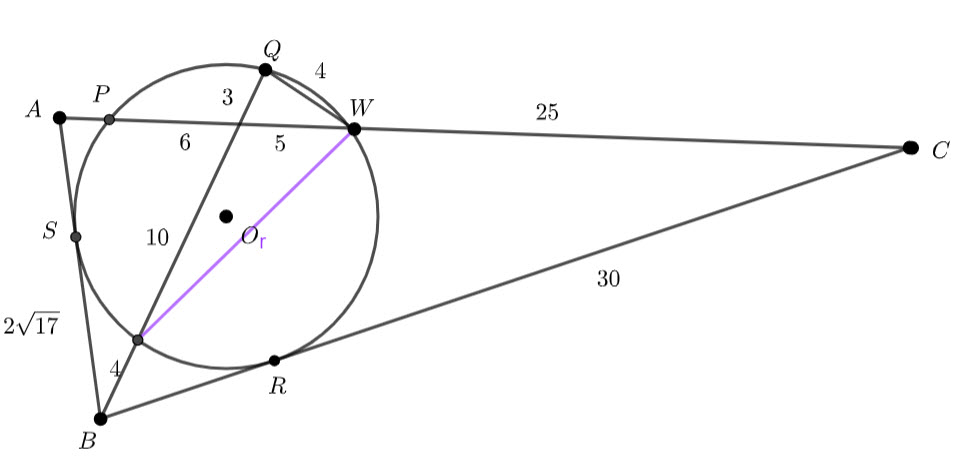
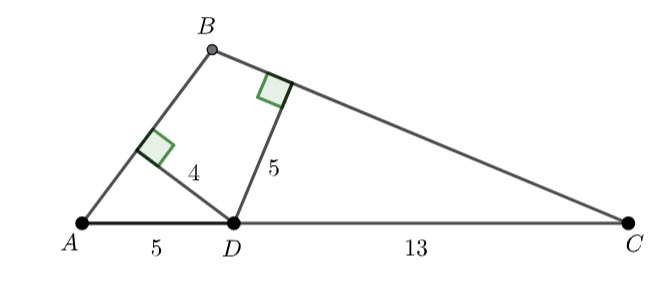
In triangle ABC, AC=18 and D is the point on AC for which AD=5. Perpendiculars drawn from D to AB and CB have lengths of 4 and 5 respectively. What is the area of triangle ABC?
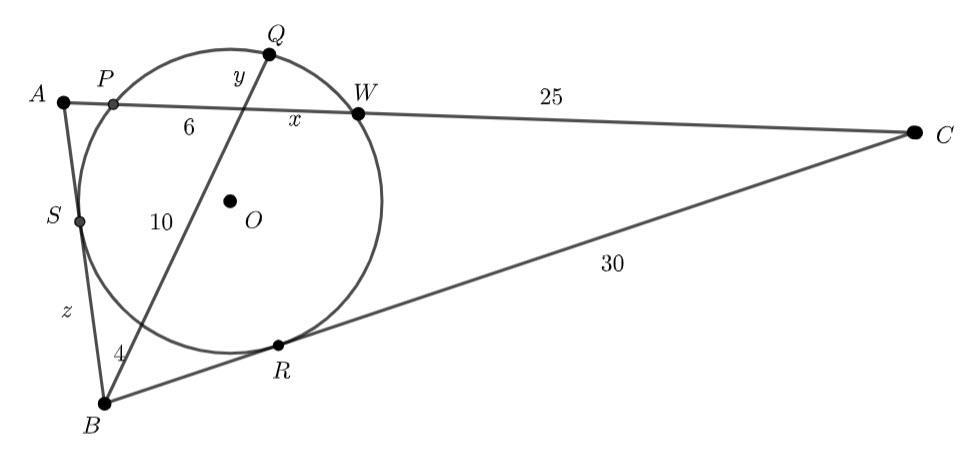
I put together a diagram (in Geogebra)
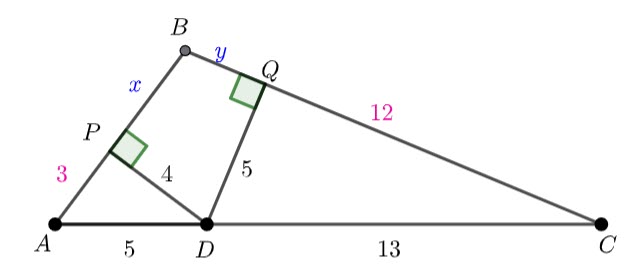
Add points P and Q

Triangle APD and triangle DQC are right angled. Using pythagoras, ![]() and
and ![]()
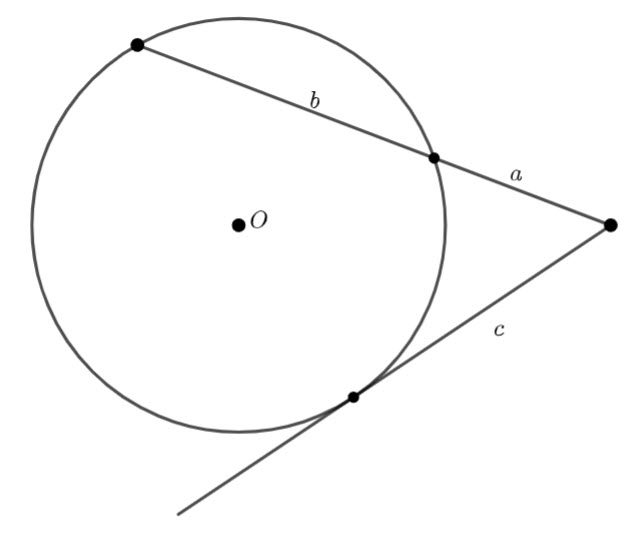
![]() is a cyclic quadrilateral and
is a cyclic quadrilateral and ![]() is the diameter. I am not sure if this is useful, but it is good to notice.
is the diameter. I am not sure if this is useful, but it is good to notice.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
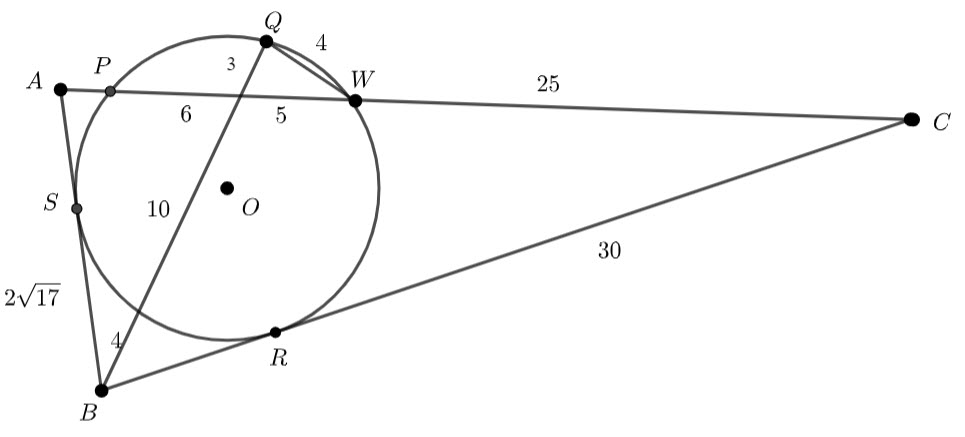
If ![]() then
then ![]()
Now,
![]()
![]()
![]()
Hence the Area is
![]()
![]()
![]()