Mean | Racquel Sanderson

Category Archives: Mean

April 13, 2025 · 9:23 am

Binomial Distribution – deriving the equation for mean (expected value)

The mean, $\mu$ of a binomial distribution is

(1) $\begin{equation*}\mu=np\end{equation*}$

where $n$ is the number of trials and $p$ is the probability of success.

For any discrete probability distribution , the expected value or mean is

(2) $\begin{equation*}E(X)=\sum_{x=0}^nxp(x)\end{equation*}$

For example, if a coin is tossed $3$ times and the number of heads is recorded, the distribution is

$X$	$0$	$1$	$2$	$3$
$P(X=x)$	$\frac{1}{8}$	$\frac{3}{8}$	$\frac{3}{8}$	$\frac{1}{8}$

$\begin{equation*}E(X)=0\times\frac{1}{8}+1\times\frac{3}{8}+2\times\frac{3}{8}+3\times{1}{8}\end{equation}$

$\begin{equation*}E(X)=\frac{12}{8}=\frac{3}{2}\end{equation}$

I want to show how the $\mu=np$ formula is derived from the general formula (equation $(2)$ ).

$\begin{equation*}E(X)=\sum^n_{x=0}xp(x)\end{equation}$

For a binomial distribution, $p(x)=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}$

$\begin{equation*}E(X)=\sum_{x=0}^nx\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\end{equation}$

$\begin{equation*}E(X)=\sum^n_{x=0}x\frac{n!}{(n-x)!x!}p^x(1-p)^{n-x}\end{equation}$

The $x$ can cancel with the $x!$ to leave $(x-1)!$ on the denominator.

$\begin{equation*}E(X)=\sum^n_{x=0}\frac{n!}{(n-x)!(x-1)!}p^x(1-p)^{n-x}\end{equation}$

Also, when $x=0 \Rightarrow xp(x)=0$ , hence the sum can start at $x=1$ .

$\begin{equation*}E(X)=\sum^n_{x=1}\frac{n!}{(n-x)!(x-1)!}p^x(1-p)^{n-x}\end{equation}$

Let $y=x-1$ and $m=n-1$

When $x=n \Rightarrow y=n+1=m$

$\begin{equation*}E(X)=\sum^{m}_{y=0}\frac{(m+1)!}{((m+1)-(y+1))!(y)!}p^{y+1}(1-p)^{(m+1)-(y+1)}\end{equation}$

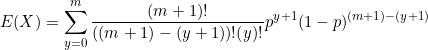
Simplify

$\begin{equation*}E(X)=\sum^{m}_{y=0}\frac{(m+1)!}{((m-y))!(y)!}p^{y+1}(1-p)^{(m-y)}\end{equation}$

$\begin{equation*}E(X)=\sum^{m}_{y=0}\frac{(m+1)m!}{((m-y))!(y)!}p^yp^1(1-p)^{(m-y)}\end{equation}$

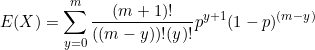
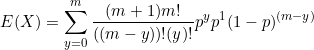
We can move $(m+1)$ and $p$ out of the sum.

$\begin{equation*}E(X)=(m+1)p\sum^{m}_{y=0}\frac{m!}{((m-y))!(y)!}p^y(1-p)^{(m-y)}\end{equation}$

$\begin{equation*}\sum^{m}_{y=0}\frac{m!}{((m-y))!(y)!}p^y(1-p)^{(m-y)}=\sum^{m}_{y=0}\begin{pmatrix}m\\y\end{pmatrix}p^y(1-p)^{(m-y)}\end{equation}$

$\begin{equation*}\sum^{m}_{y=0}\begin{pmatrix}m\\y\end{pmatrix}p^y(1-p)^{(m-y)}=1\end{equation}$

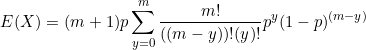
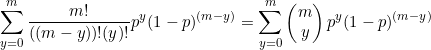
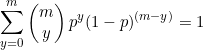
As it is the sum of the probabilities of a binomial distribution with $m$ trials.

Hence $E(X)=(m+1)p=np$

Next, deriving the variance formula for a binomial distribution.