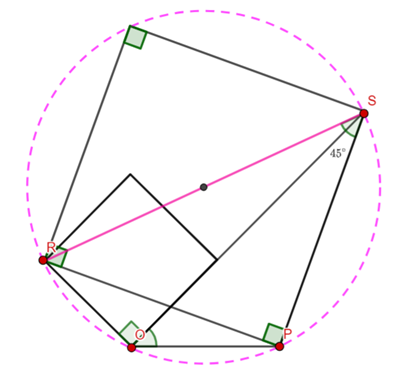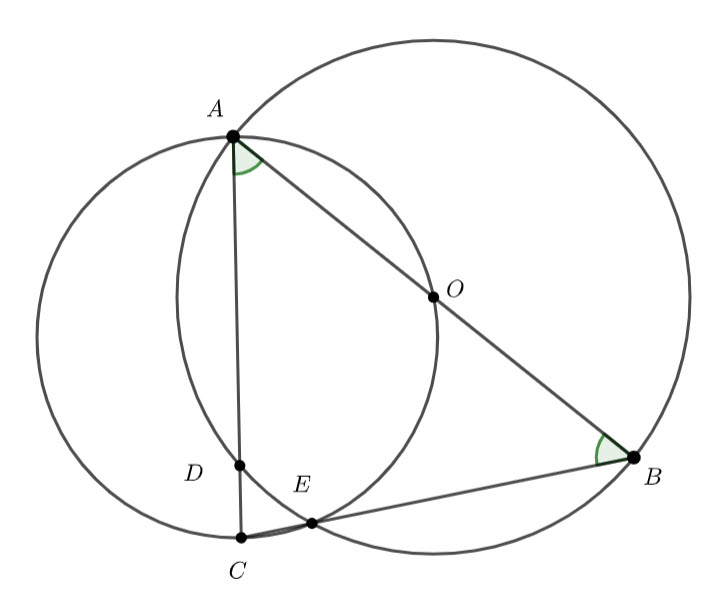
In the above diagram ![]() is the centre of the larger circle.
is the centre of the larger circle. ![]() and
and ![]() are points on the circumference of the larger circle.
are points on the circumference of the larger circle. ![]() and
and ![]() are points on the circumference of the smaller circle. Show that
are points on the circumference of the smaller circle. Show that ![]() .
. ![]() and
and ![]() are straight lines.
are straight lines.
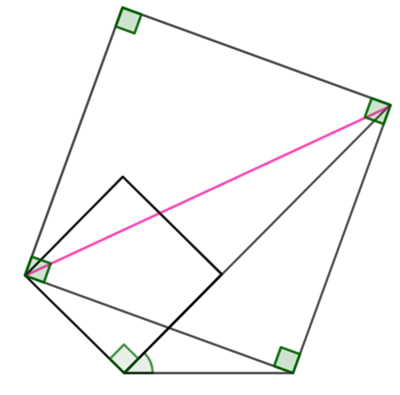
![]() (radii of the larger circle)
(radii of the larger circle)
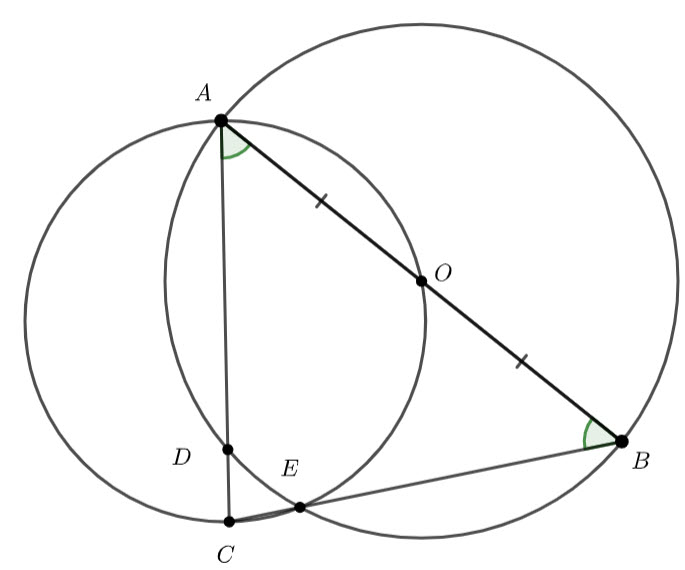
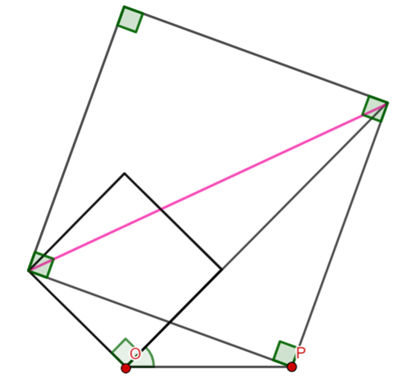
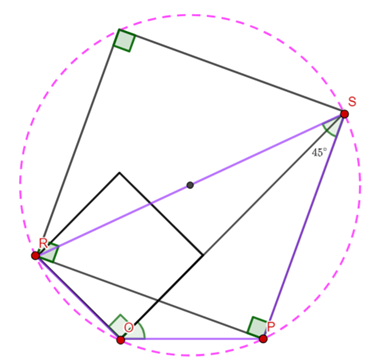
At a line from ![]() to
to ![]() (it is also a radius of the larger circle)
(it is also a radius of the larger circle)
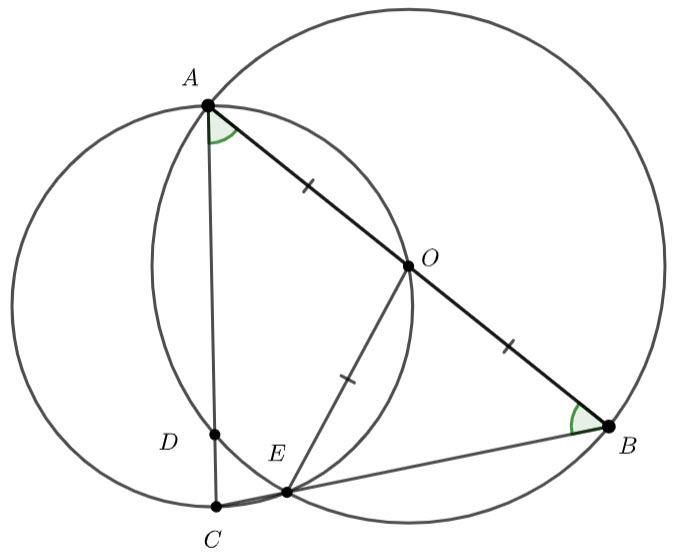
Let ![]() .
.
![]() is a cyclic quadrilateral.
is a cyclic quadrilateral.
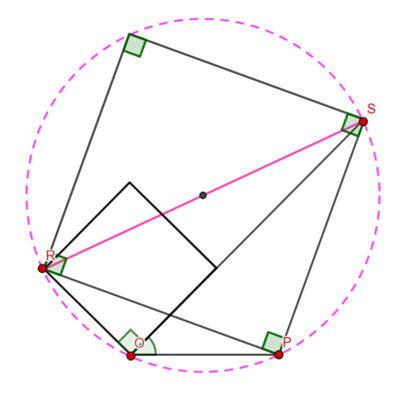
Hence, ![]() (
(![]() is a cyclic quadrilateral)
is a cyclic quadrilateral)
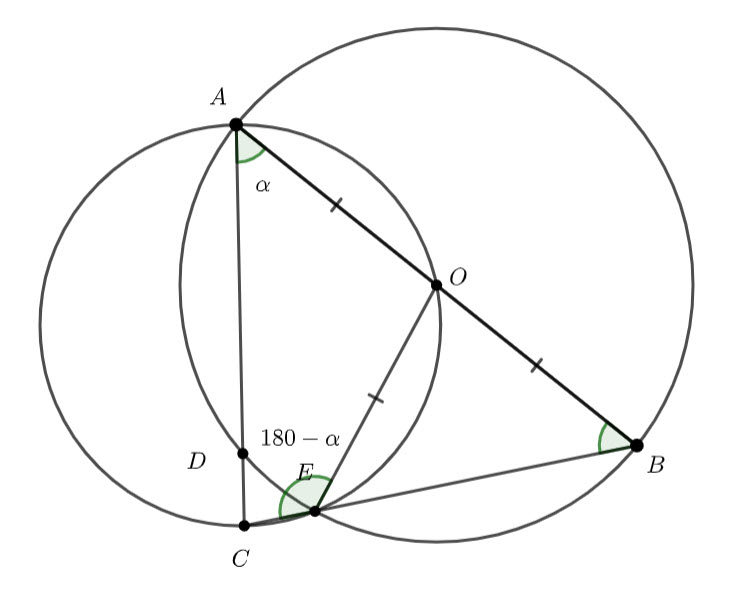
As ![]() is a straight line
is a straight line ![]() .
.
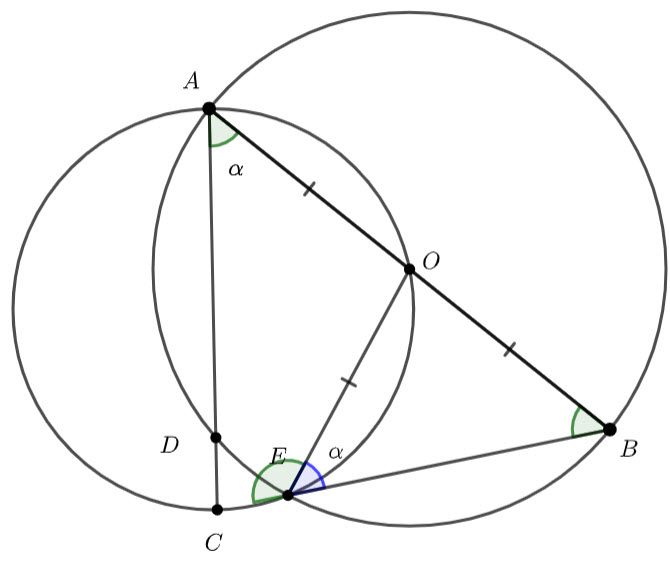
![]() is an isosceles triangle.
is an isosceles triangle.
Therefore, ![]()
Therefore ![]()