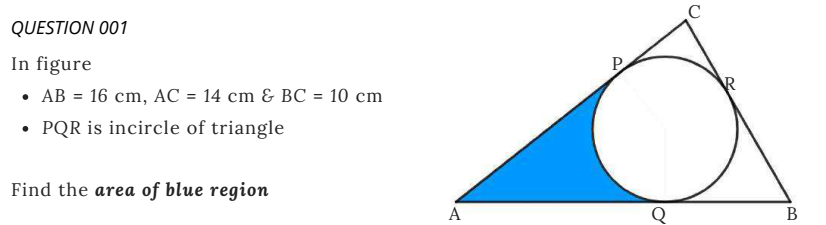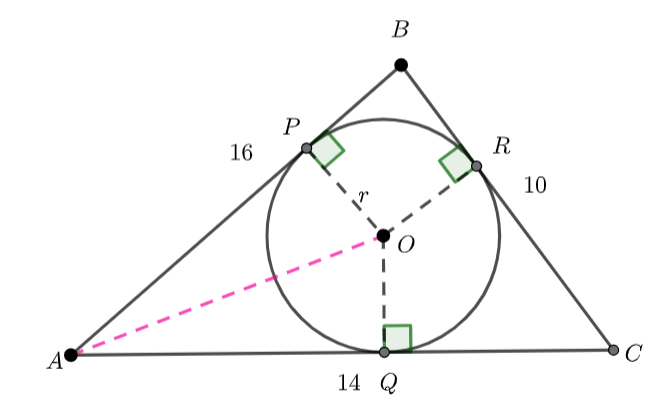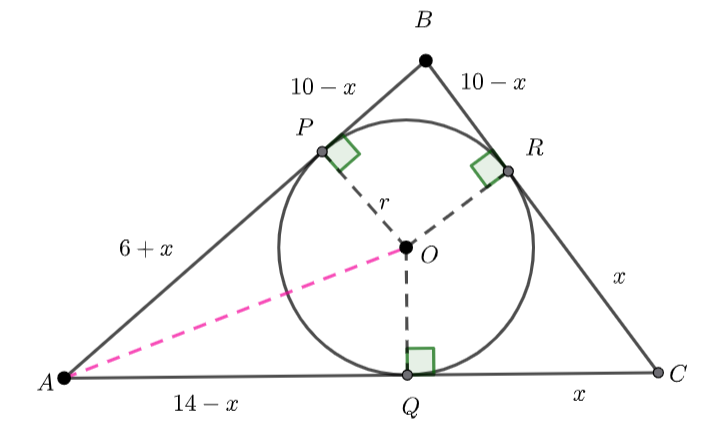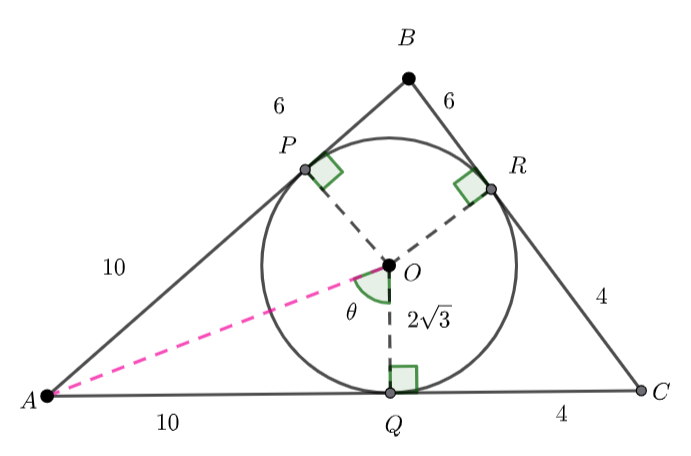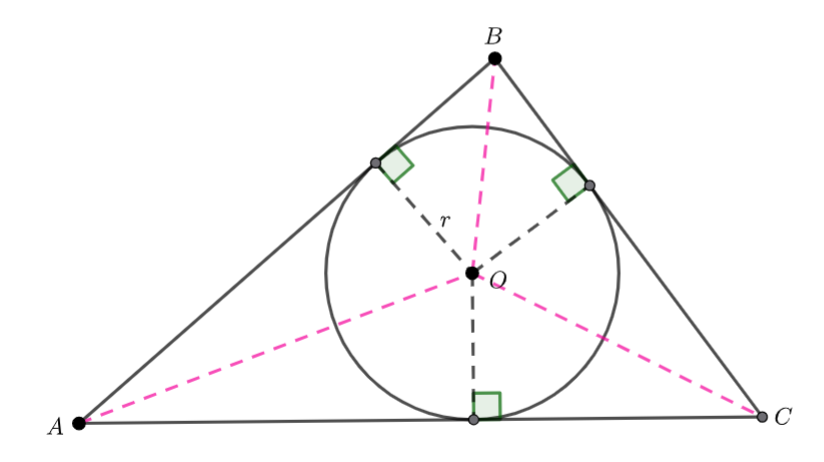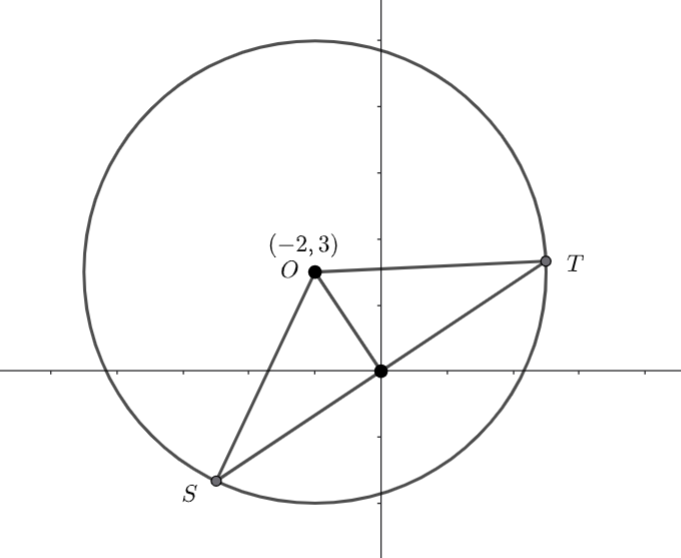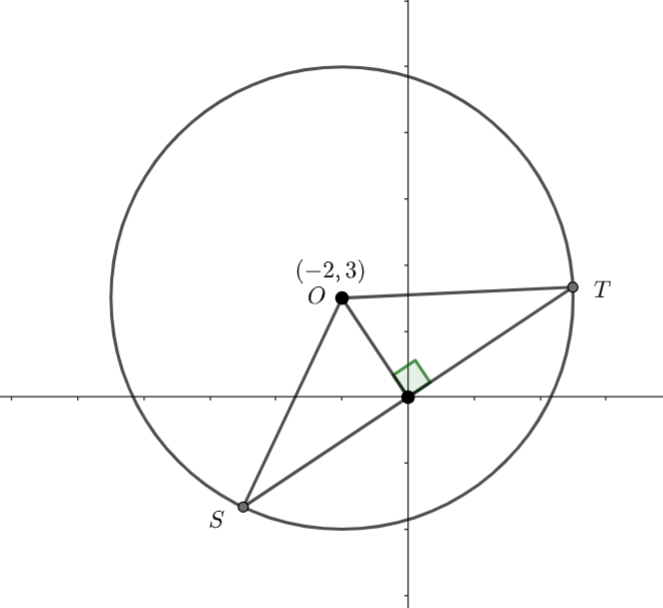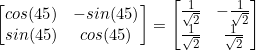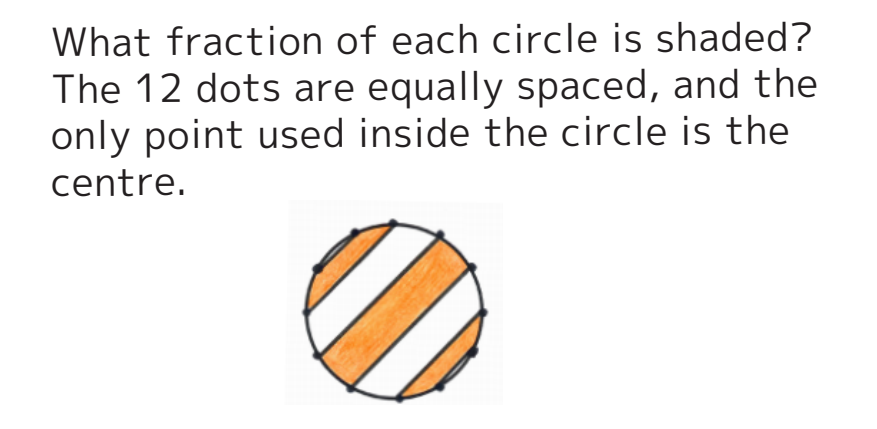
Band ![]() and
and ![]() have the same area.
have the same area.
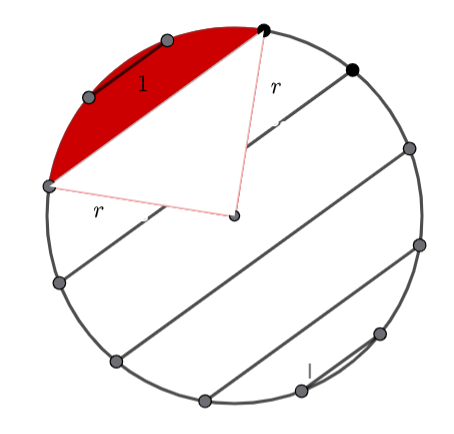
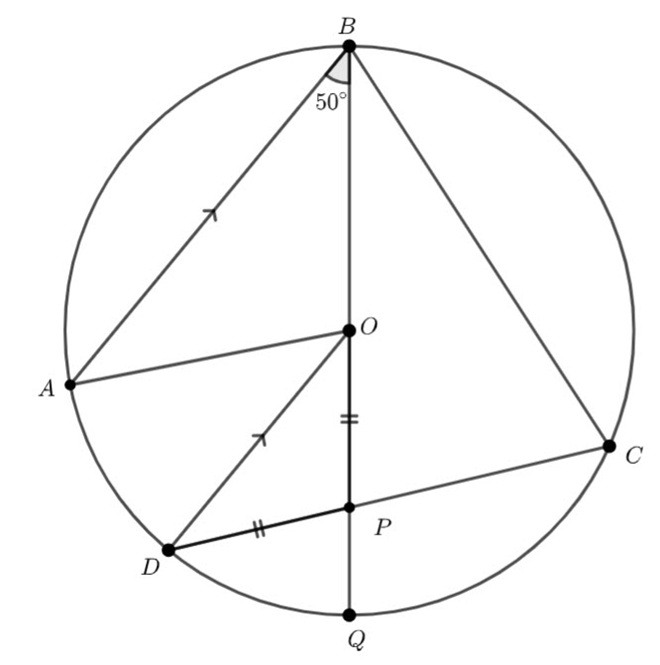
We want to find the area of the shaded segment.
As the dots are equally spaced, the sector’s angle is ![]()
Remember the area of a segment is ![]() where the angle measurement is in radians.
where the angle measurement is in radians.
(1) ![]()
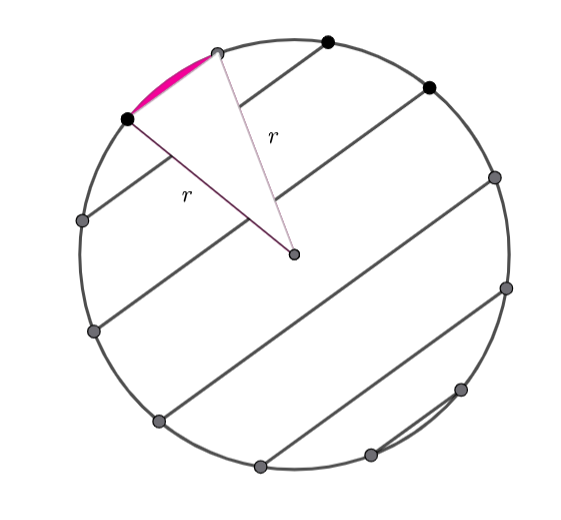
We want to find the area of the shaded segment.
As the dots are equally spaced, the sector’s angle is ![]()
(2) ![]()
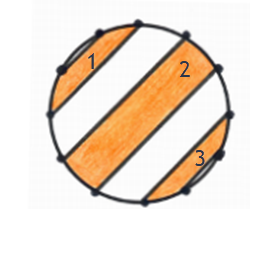
The area of band ![]() is equation
is equation ![]() equation
equation ![]() .
.
(3) ![]()
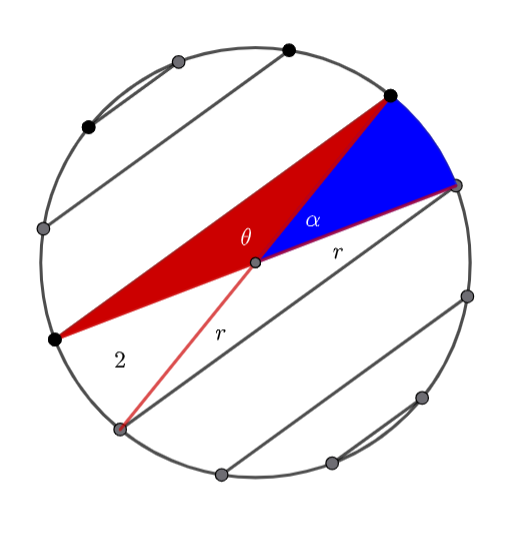
Band 2 consists of two congruent triangles and two congruent sectors.
![]()
(4) ![]()
Hence the shaded area is ![]()
The area of the circle is ![]()
Hence the fraction of the shaded area is ![]()