The logistic differential equation
![]()
where ![]() is the growth parameter and
is the growth parameter and ![]() is the carrying capacity.
is the carrying capacity.
And the maximum rate of increase happens when ![]()
![]()
![]()
![]()
I am going to separate the denominator on the left hand side
Hence, When When |
So our equation is,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
When ![]() ,
,
![]()
The equation is now
![]()
![]()
![]()
![]()
![]()
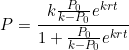
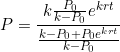
![]()
Divide by ![]()
![]()
![]()
Proving the Maximum Rate of Increase Happens When 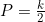
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence ![]() or
or ![]()
(1) ![]()
Substitute ![]() into equation
into equation ![]()
![]()
Hence, not a maximum.
Substitute ![]() into equation
into equation ![]()
![]()
![]()
![]()
![]() For all values of
For all values of ![]() and
and ![]() .
.
Hence maximum when ![]()
We will look at a worked example in the next post.