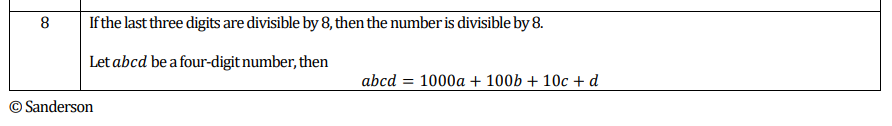Category Archives: Arithmetic

September 23, 2024 · 3:11 am

Cats and Dogs

In my town 10% of the dogs think they are cats and 10% of the cats think they are dogs. All the other cats and dogs are perfectly normal. When all the cats and dogs in my town were rounded up and subjected to a rigorous test, 20% of them thought they were cats. What percentage of them really were cats?
Hamilton Olympiad 2003 B4 – The Ultimate Mathematical Challenge

Let $x$ be the number of cats and $y$ be the number of dogs.
Then $0.9x+0.1y$ think they are cats.
But we also know 20% of the total think they are cats.
$0.2(x+y)$
Therefore, $0.9x+0.1y=0.2(x+y)$
$0.9x+0.1y=0.2x+0.2y$
$0.7x=0.1y$
$7x=y$
Percentage of cats is $\frac{x}{x+y}\times100$
Substitute $7x$ for $y$
$\frac{x}{x+7x}\times100=\frac{x}{8x}\times100=\frac{1}{8}\times100=12.5%$
$\therefore 12.5$ % of the animals are cats

Leave a Comment

Filed under Algebra, Arithmetic, Percentages, Simplifying fractions, UK Mathematics Challenge

Tagged as Fractions, percent, uk maths challenge

July 16, 2024 · 7:35 am

Australian Mathematics Competition – Polynomial Question

I came across this question from the 2010 Senior Australian Mathematics Competition:

A polynomial $f$ is given. All we know about it is that all its coefficients are non-negative integers, $f(1)=6$ and $f(7)=3438$ . What is the value of $f(3)$
Australian Mathematics Competition 2006-2012

I thought ‘excellent, a somewhat hard polynomial question for my students’ and then I tried it. Now I know why only 1% of students got it correct.

As we don’t know the order of the polynomial, let

$f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0$

We know all of the coefficients are greater than or equal to zero. We also know

$f(1)=a_n+a_{n-1}+...+a+a_0=6$

Which means that all of the coefficients are between zero and six

$0\le{a_n}\le{6}$

We have also been given $f(7)$

$f(7)=7^na_n+7^{n-1}a_{n-1}+ ... +7a+1=3438$

As all of the coefficients are between zero and six, this is $3438$ written in base 7.

Let’s calculate a few powers of 7

	Powers of 7
$7^0$	1
$7^1$	7
$7^2$	49
$7^3$	343
$7^4$	2401
$7^5$	16807

Hence $3438$ written in base $7$ is $13011$

Therefore $f(x)=x^4+3x^3+x+1$

$f(3)=3^4+3\times3^3+3+1$

$f(3)=81+81+4$

$f(3)=166$

I really like this question. I think it could work well as a class extension activity with a bit of scaffolding.

Leave a Comment

Filed under Number Bases, Polynomials

Tagged as base 7, number bases, Polynomials

May 12, 2024 · 11:50 am

Fractions to decimals

People usually know some fractions as decimals, for example

$\frac{1}{4}=0.25\ \textnormal{or }\frac{4}{5}=0.8$

And denominators that are powers of ten are also easy,

$\frac{47}{100}=0.47\ \textnormal{or }\frac{256}{1000}=0.256$

But what if it is something else? One that you don’t know. For example,

$\frac{5}{12}\ \textnormal{or }\frac{15}{37}$

I like to do these as a long division

Leave a Comment

Filed under Arithmetic, Decimals, Fractions

Tagged as decimals, Fractions, fractions to decimals

April 14, 2024 · 6:35 am

Divisibility Rules – Integers 1 to 10

I think it’s useful to knot the divisibility rules, at least up to ten. Although, let’s face it, 7 is a bit tricky.

Divisibility Rules pdf

Leave a Comment

Filed under Arithmetic, Divisibility

Tagged as Arithmetic, Divisibility rules

As numbers	As Powers of 7
$3438=1\times2401+1037$	$3438=1\times7^4+1037$
$1037=3\times343+8$	$1037=3\times7^3+8$
$8=1\times7+1$	$8=1\times7^1+1$
$1=1\times1$	$1=1\times7^0$

Category Archives: Arithmetic

Cats and Dogs

Australian Mathematics Competition – Polynomial Question

Fractions to decimals

Divisibility Rules – Integers 1 to 10

Recent Posts

Categories

Archives