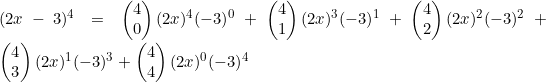Binomial Expansion Theorem

Category Archives: Binomial Expansion Theorem

March 5, 2025 · 2:00 am

My Year 11 Mathematics Methods students are working on the Binomial Expansion Theorem.

But before we get onto that, remember Pascal’s triangle

Now we can use combinations to find the numbers in each row. For example, $1 4 6 4 1$ is $\begin{pmatrix}4\\0\end{pmatrix}=1, \begin{pmatrix}4\\1\end{pmatrix}=4, \begin{pmatrix}4\\2\end{pmatrix}=6, \begin{pmatrix}4\\3\end{pmatrix}=4, \begin{pmatrix}4\\4\end{pmatrix}=1$

As you can see, the coefficients are the row of pascal’s triangle corresponding to the power. So $(x+y)^6$ would have co-efficients from the sixth row of the table $1, 6, 15, 20, 15, 6, 1$ .

To generalise

$(x+y)^n=\begin{pmatrix}n\\0\end{pmatrix}x^ny^0+\begin{pmatrix}n\\1\end{pmatrix}x^{n-1}y^1+\begin{pmatrix}n\\2\end{pmatrix}x^{n-2}y^2+ ...+\begin{pmatrix}n\\n-1\end{pmatrix}x^1{y^{n-1}+\begin{pmatrix}n\\n\end{pmatrix}x^0y^n$

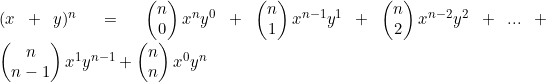
Which we can condense to

$(x+y)^n=\Sigma_{i=0}^n \begin{pmatrix}n\\i\end{pmatrix}x^{n-i}y^i$

Worked Examples

$(1)$ Expand $(2x-3)^4$

$(2x-3)^4=\begin{pmatrix}4\\0\end{pmatrix}(2x)^4(-3)^0+\begin{pmatrix}4\\1\end{pmatrix}(2x)^3(-3)^1+\begin{pmatrix}4\\2\end{pmatrix}(2x)^2(-3)^2+\begin{pmatrix}4\\3\end{pmatrix}(2x)^1(-3)^3+\begin{pmatrix}4\\4\end{pmatrix}(2x)^0(-3)^4$
$(2x-3)^4=16x^4-96x^3+216x^2-216x+81$

$(2)$ Find the co-efficient of the $x^3$ term in the expansion of $(2-5x)^5$ .

Remember $(x+y)^n=\Sigma_{i=0}^n \begin{pmatrix}n\\i\end{pmatrix}x^{n-i}y^i$ , the $x^3$ is when $i=3$
$\begin{pmatrix}5\\3\end{pmatrix}(2)^2(-5)^3=10\times 2\times -125=-5000$

$(3)$ Find the constant term in the expansion of $(x^2+\frac{3}{x^4})^6$

We need to find the term where the $x$ ‘s cancel out. Each term is $\begin{pmatrix}6\\i\end{pmatrix}(x^2)^{6-i}(\frac{3}{x^4})^i$ .
$\begin{pmatrix}6\\i\end{pmatrix}(x^{12-2i})(3^ix^{-4i})$ .
We need $12-2i-4i=0$ , hence $i=2$
Therefore, the co-efficient is $\begin{pmatrix}6\\2\end{pmatrix}\times3^2=135$

Puzzle Page 2

If $x^2-3x+1=0$ , then find $x^5+\frac{1}{x^5}$ .

My first thought was to solve for $x$ , but it doesn’t factorise easily, and I didn’t want to find the fifth power of an expression involving surds $(x=\frac{3\pm \sqrt{5}}{2})$ , there must be an easier way.

Because $x\neq0$ , we can divide by $x$

$\begin{equation*}x-3+\frac{1}{x}=0\end{equation}$

Hence

(1) $\begin{equation*}x+\frac{1}{x}=3\end{equation*}$

What is the expansion of $(x+\frac{1}{x})^5$ ?

Using the binomial expansion theorem

$\begin{equation*}(x+\frac{1}{x})^5=x^5+5x^4(\frac{1}{x})+10x^3(\frac{1}{x^2})+10x^2(\frac{1}{x^3})+5x(\frac{1}{x^4})+\frac{1}{x^5}\end{equation}$

$\begin{equation*}(x+\frac{1}{x})^5=x^5+\frac{1}{x^5}+5(x^3+\frac{1}{x^3})+10(x+\frac{1}{x})\end{equation}$

Therefore

(2) $\begin{equation*}x^5+\frac{1}{x^5}=(x+\frac{1}{x})^5-5(x^3+\frac{1}{x^3})-10(x+\frac{1}{x})\end{equation*}$

Let’s do it again for $x^3+\frac{1}{x^3}$

$\begin{equation*}(x+\frac{1}{x})^3=x^3+3x^2(\frac{1}{x})+3x(\frac{1}{x^2})+\frac{1}{x^3}\end{equation}$

(3) $\begin{equation*}x^3+\frac{1}{x^3}=(x+\frac{1}{x})^3-3(x+\frac{1}{x})\end{equation*}$

Substitute $3$ into $2$

$\begin{equation*}x^5+\frac{1}{x^5}=(x+\frac{1}{x})^5-5((x+\frac{1}{x})^3-3(x+\frac{1}{x}))-10(x+\frac{1}{x})\end{equation}$

Remember $x+\frac{1}{x}=3$

Therefore

$\begin{equation*}x^5+\frac{1}{x^5}=3^5-5(3^3)+15\times3-10\times3\end{equation}$

$\begin{equation*}x^5+\frac{1}{x^5}=243-135+45-30=123\end{equation}$

This would be a good extension question for students learning the binomial expansion theorem. We also use this technique for trigonometric identities using complex numbers.

Expression	Expansion	Co-efficients
$(x+y)^2$	$x^2+2xy+y^2$	$1, 2, 1$
$(x+y)^3$	$x^3+3x^2y+3xy^2+y^3$	$1, 3, 3, 1$
$(x+y)^4$	$x^4+4x^3y+6x^2y^2+4xy^3+y^4$	$1, 4, 6, 4, 1$

Category Archives: Binomial Expansion Theorem