A circle of radius
, is inscribed within an isosceles triangle
.
. Given that
is acute, find the ratio of the area of the circle to that of triangle
.
Mathematics Specialist 3AB Question15 page 55
I came across this question while searching for an area of sectors and segments question.
Here’s a diagram
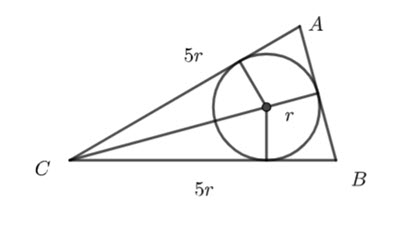
We know ![]() are tangents to the circle. Because the triangle is isosceles, the distance from
are tangents to the circle. Because the triangle is isosceles, the distance from ![]() to the circle is the same as the distance from
to the circle is the same as the distance from ![]() to the circle.
to the circle.
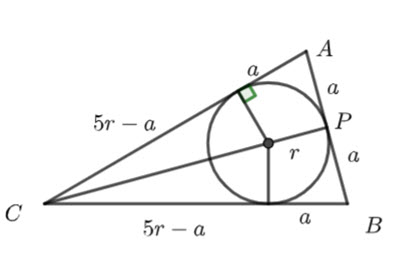
![]() is perpendicular to
is perpendicular to ![]() (because the triangle is isosceles).
(because the triangle is isosceles).
Because it is proportional, i.e. ![]() and
and ![]() , we can let
, we can let ![]()
Let ![]()
(1) ![]()
but ![]() also equals
also equals
(2) ![]()
Set equation ![]() equal to equation
equal to equation ![]()
![]()
Square both sides
![]()
Expand and simplify
![]()
![]()
Divide by ![]()
![]()
![]()
Square both sides
![]()
![]()
![]()
I solved this using a graphics calculator
![]()
We can reject ![]() ,
, ![]() , and
, and ![]() . If
. If ![]() , there isn’t a triangle, and if
, there isn’t a triangle, and if ![]()
![]() is not acute.
is not acute.
Hence the area of triangle ![]()
![]()
(3) ![]()
(4) ![]()
Hence, equation ![]() divided by equation
divided by equation ![]() is
is
![]()
Perhaps I approached this question in the wrong way. Is there an easier process?
