Ming, a former high school student and now a successful business owner, wishes to set up a perpetuity of $6000 per year to be paid to a deserving student from her school. The perpetuity is to be paid at the start of the year in one single payment.
(a) A financial institution has agreed to maintain an account for the perpetuity paying a fixed rate of 5.9% p.a. compounded monthly. Show that an amount of $98 974, to the nearest dollar, is required to maintain this perpetuity.
(b) Ming allows herself five years to accumulate the required $98 974 by making regular quarterly payments into an account paying 5.4% p.a. compounded monthly. Determine the quarterly payment needed to reach the required amount after five years if Ming starts the account with an initial deposit of $1000.
SCSA 2017 CA 8
(a) For a perpetuity, we want the interest to equal the payment.
Remember the compound interest formula is
Where 
is the principal, 
is the interest rate (as a percent), 
is the number of compounding periods in a year, and 
is the time.
Therefore an amount of $98 974 is required to maintain this perpetuity
For part (b) I will use the Finance Solver on a Classpad (Casio).
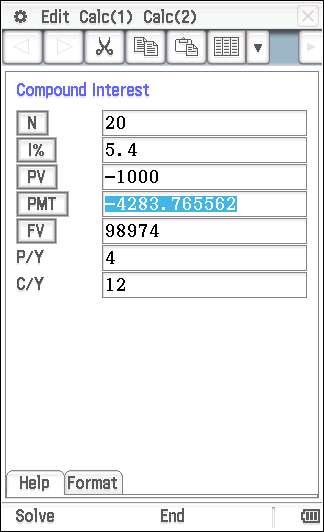 | N is the number of payments,  PV is the principal value. To get the signs correct it is helpful to think about the direction of the flow of the money. The $1000 is going away from Ming so it is negative. FV is the future value. P/Y is the number of payments per year (quarterly so 4) C/Y is the number of compounding periods per year (monthly so 12). PMT is the payment |
The quarterly payments are $4283.77.