As I have done a cosine rule proof, I thought I should also do a sine rule proof.
![]()
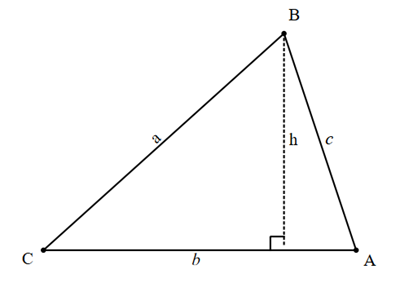
From the above diagram, we can find ![]() in two ways.
in two ways.
Set equation 1 equal to equation 2
![]()
![]() or
or ![]()
We could have put the altitude of the triangle from vertex A
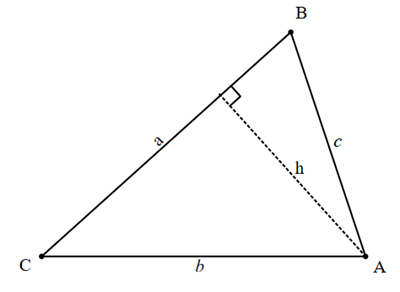
Following the same process as above
Set equation 3 equal to equation 4.
![]()
![]()
Now ![]() therefore
therefore
![]() or
or ![]()
