![]()
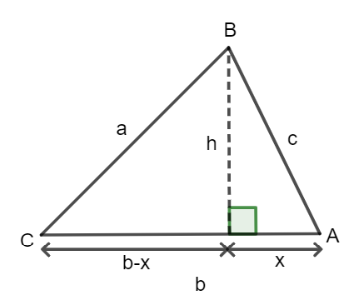
From the diagram above
![]()
![]()
![]()
![]()
(1) ![]()
From the diagram above, we can see
![]()
(2) ![]()
Substitute equation 2 into equation 1
![]()
It can also be handy to have the angle version
![]()
![]()

From the diagram above
![]()
![]()
![]()
![]()
(1) ![]()
From the diagram above, we can see
![]()
(2) ![]()
Substitute equation 2 into equation 1
![]()
It can also be handy to have the angle version
![]()
Filed under Non-Right Trigonometry, Right Trigonometry, Trigonometry, Uncategorized
Pingback: Proof of the Sine Rule | Racquel Sanderson