
I am came across this problem and was fascinated. It’s from this book

At first I went straight to the 14-sided polygon, and tried to draw the diamonds (parallelograms), but then I thought let’s start smaller and see if there is a pattern.
Clearly a square contains 1 diamond (itself).
Pentagon
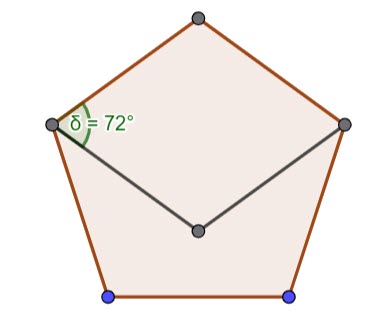
It’s not possible with a pentagon.
Hexagon
A hexagon has 6 diamonds
Septagon
I am guessing it’s not possible to fill a regular 7-sided shape with diamonds
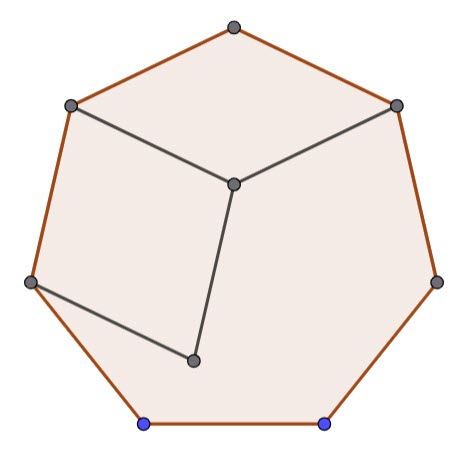
It’s not possible with odd numbers of sides. Regular polygons with an odd number of sides have no parallel sides, so we can’t cover it with rhombi (which have opposite sides parallel).
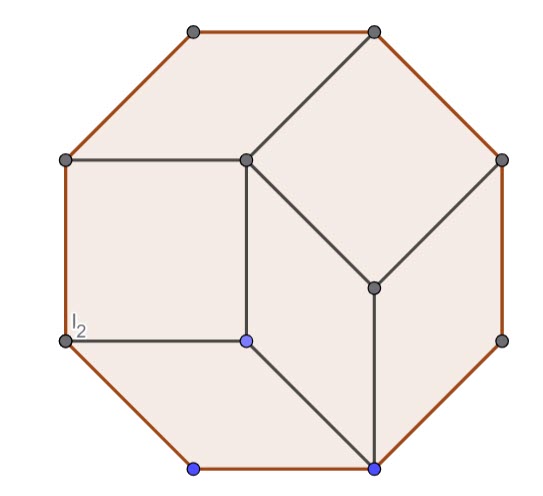
Octagon
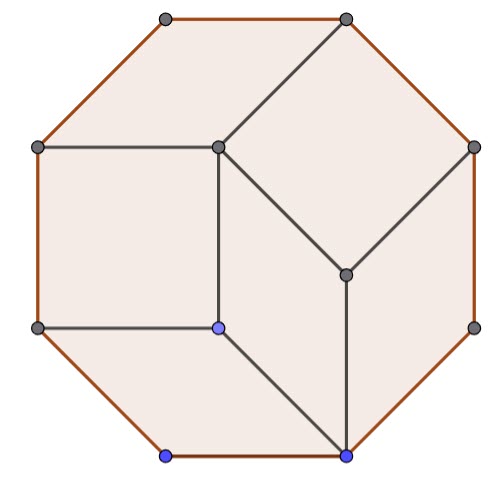
An octagon has 6 diamonds.
We know a decoagon has 10 diamonds (from the question)
Let’s put together what we know
| Diamonds |
These are the triangular numbers, so when ![]() the number of diamonds is
the number of diamonds is ![]() , and for
, and for ![]() it’s
it’s ![]() .
.
We can work out a rule for calculating the number of diamonds given the number of sides.
Because the difference in the ![]() values is not
values is not ![]() , I am going to get
, I am going to get ![]() and
and ![]() in terms of
in terms of ![]() and then combine the two equations.
and then combine the two equations.

From the above table, ![]()
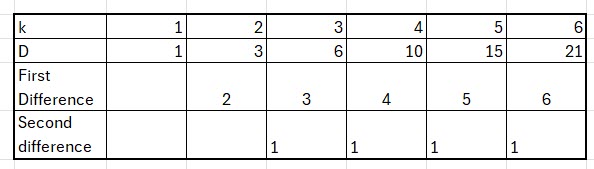
We know this rule is quadratic as the second difference is constant, hence
![]()
![]()
(1) ![]()
![]()
(2) ![]()
Solve simultaneously, subtract equation ![]() from equation
from equation ![]()
(3) ![]()
Substitute for ![]() into equation
into equation ![]()
![]()
![]() , therefore
, therefore ![]()
We know ![]() hence
hence ![]()
Hence ![]()
![]()
![]()
Let’s test our rule for ![]()
![]()
