I am going to use the same example as I did for Method One (Disc or Washer Method).
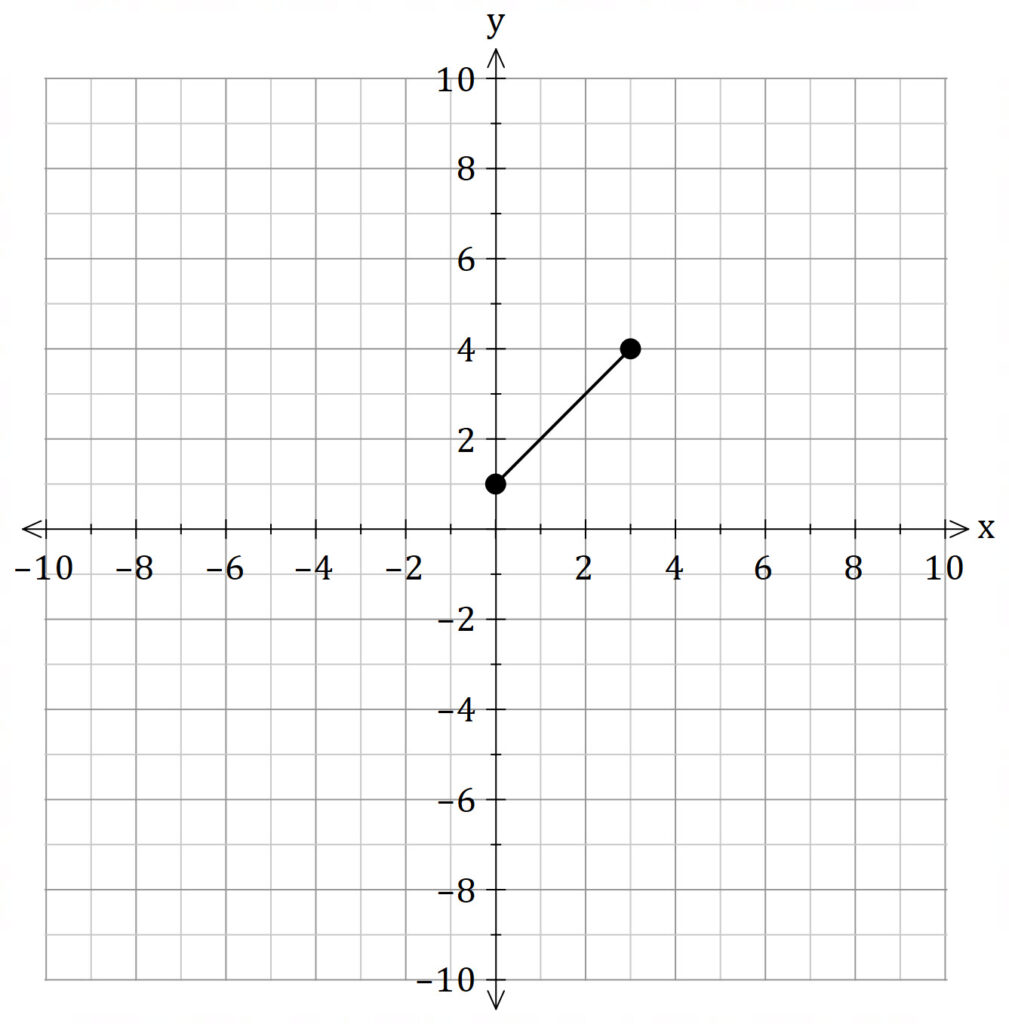
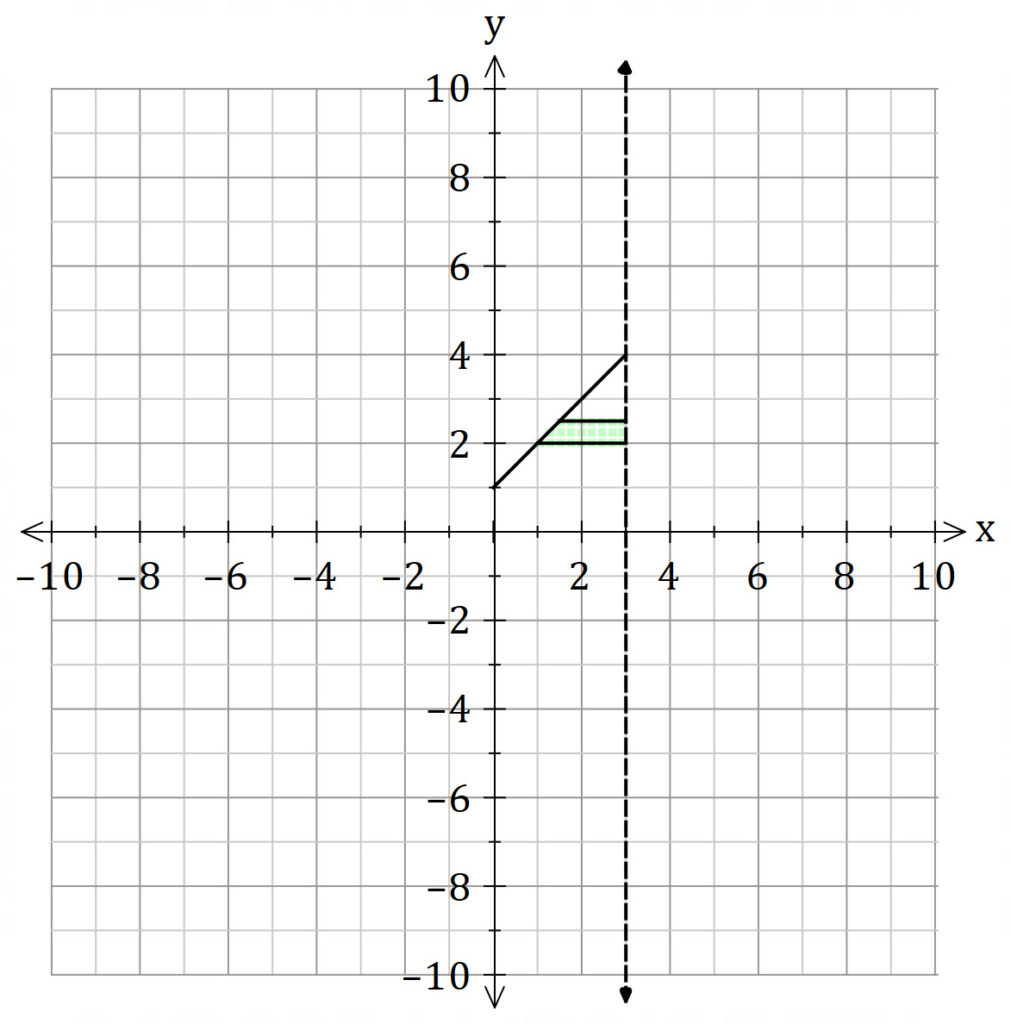
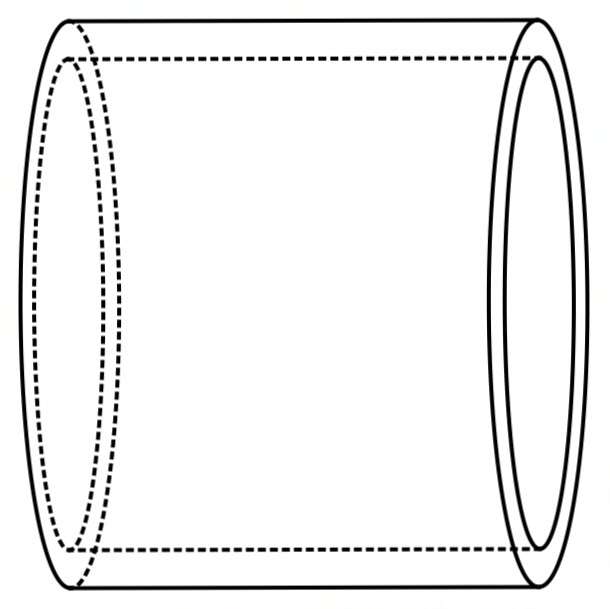
If we rotate the shaded region about the ![]() axis, we get an open hollow cylinder (like a pipe).
axis, we get an open hollow cylinder (like a pipe).
The width of the integral is ![]() and the midpoint is
and the midpoint is ![]() .
.
The height of the cylinder is ![]() , but we need it in terms of
, but we need it in terms of ![]() , hence
, hence ![]()
The volume of the hollow cylinder is the volume of the outer cylinder subtract the volume of the inner cylinder.
![]()
![]()
Which we can expand using a difference of squares.
![]()
![]()
![]()
The volume of the entire sold will be
![]()
As ![]()
![]()
Even though we are rotating the line about the ![]() axis, we are integrating with respect to the
axis, we are integrating with respect to the ![]() axis.
axis.
Example
Find the volume of the solid generated by revolving the region between ![]() and
and ![]() about the
about the ![]() axis.
axis.
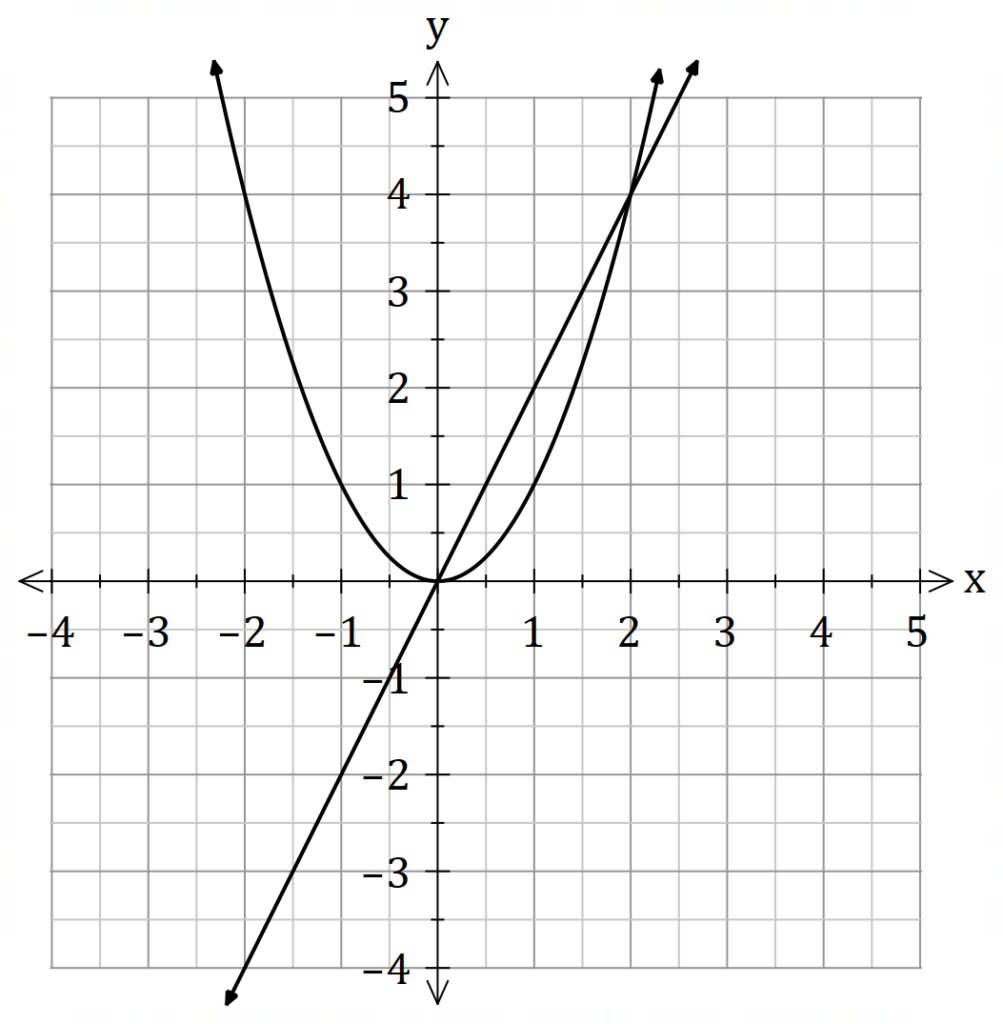
If we are rotating about the ![]() axis, we will integrate with respect to
axis, we will integrate with respect to ![]() .
.
![]()
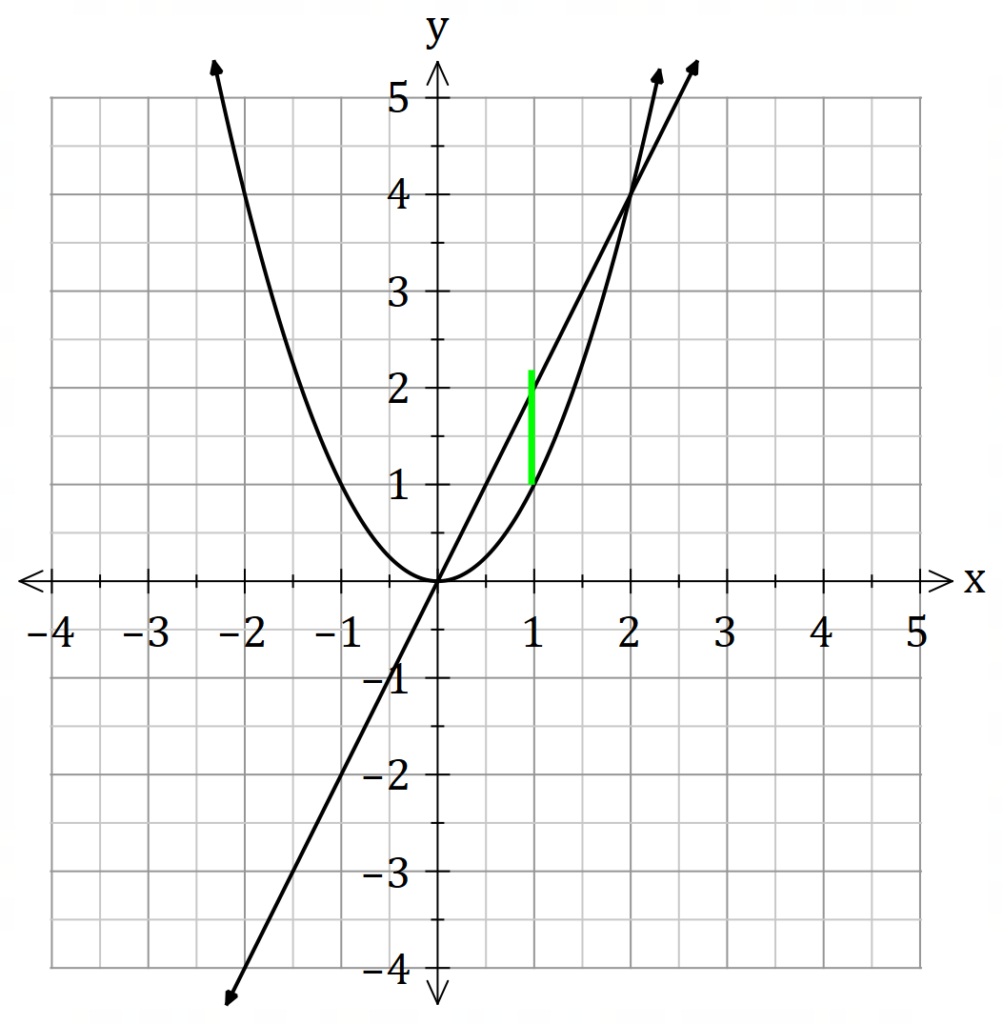

Hence
![]()
![]()
![]()
![]()
![]()
![]()
Let’s check with method one.
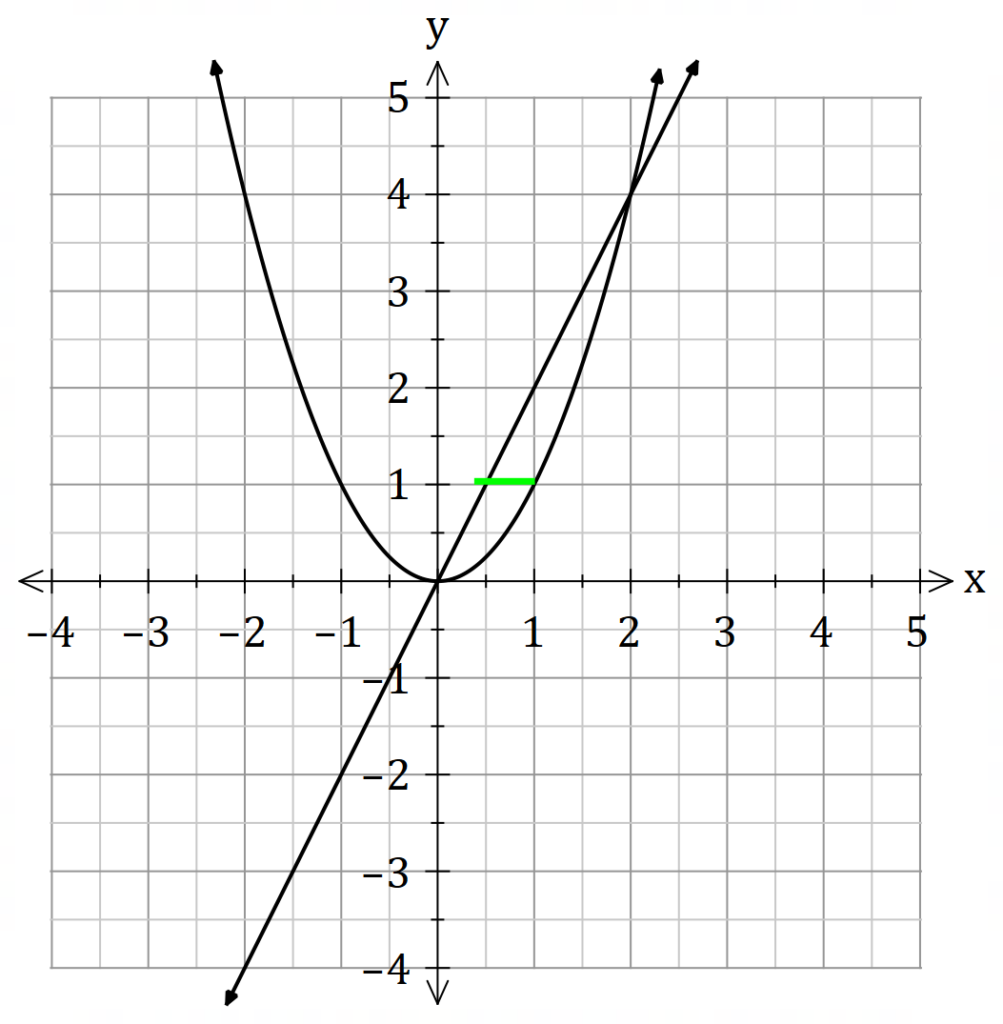
![]() and
and ![]()
![]()
![]()
![]()
![]()
I try to pick the method that makes the integration easier.

Pingback: Volume of revolution about a line that is not an axis | Racquel Sanderson