Finding the area of a regular polygon when you know the side length
Find the area of an ![]() sided regular polygon if you know the side length,
sided regular polygon if you know the side length, ![]() .
.
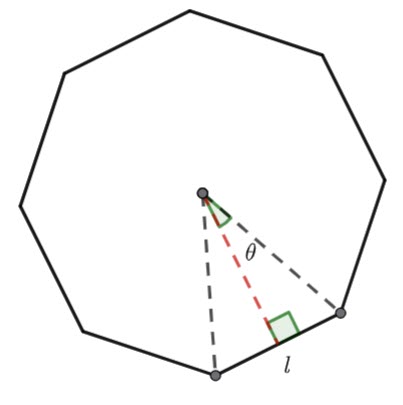
Find the ![]() of the triangle in terms of
of the triangle in terms of ![]() and theta.
and theta.
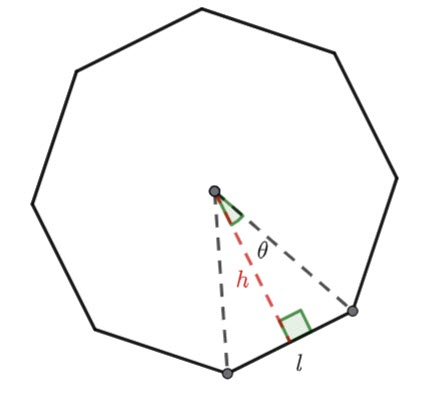
![]()
![]()
Remember the area of a triangle is ![]()
Hence, ![]()
And ![]()
Therefore ![]()
There are ![]() triangles in an
triangles in an ![]() sided polygon
sided polygon
(1) ![]()
| Find the area of a hexagon with side length 10cm. |
Finding the area of a polygon if you know the inradius or the apothem
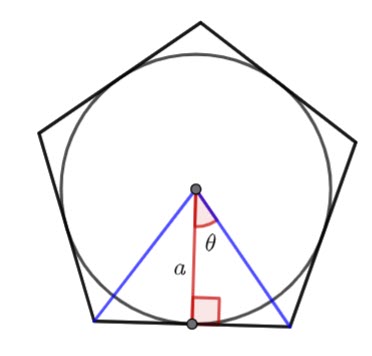
The apothem and the inradius are the same. It is the radius of the incircle.
Find the area of the triangle in terms of ![]() and theta.
and theta.
![]()
![]()
![]()
![]()
And ![]()
Hence for an ![]() sided polygon
sided polygon
(2) ![]()
| Find the area of a regular pentagon with apothem 4.5cm |
Finding the area of a regular polygon given the circumradius
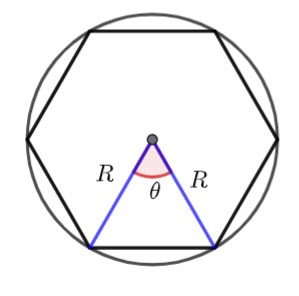
The circumradius is the radius of the circumscribed circle (![]() in the diagram above)
in the diagram above)
Remember the area of triangle formula
![]()
![]()
![]()
Hence, ![]()
Hence, for an ![]() sided polygon
sided polygon
(3) ![]()
| Find the area of a regular octagon inscribed in a circle of radius 10cm. |
