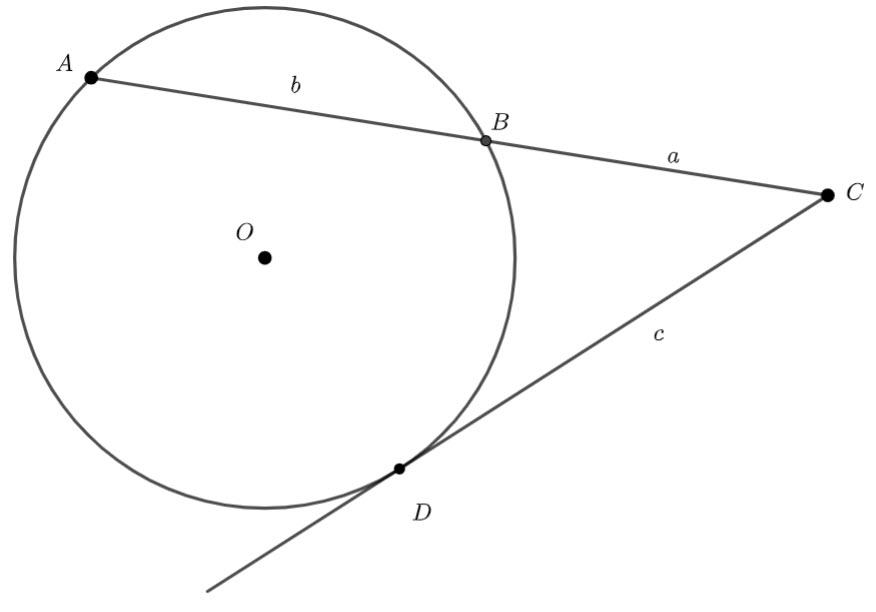
![]() is a tangent to the circle.
is a tangent to the circle.
Prove ![]()
I am going to add two chords to the circle
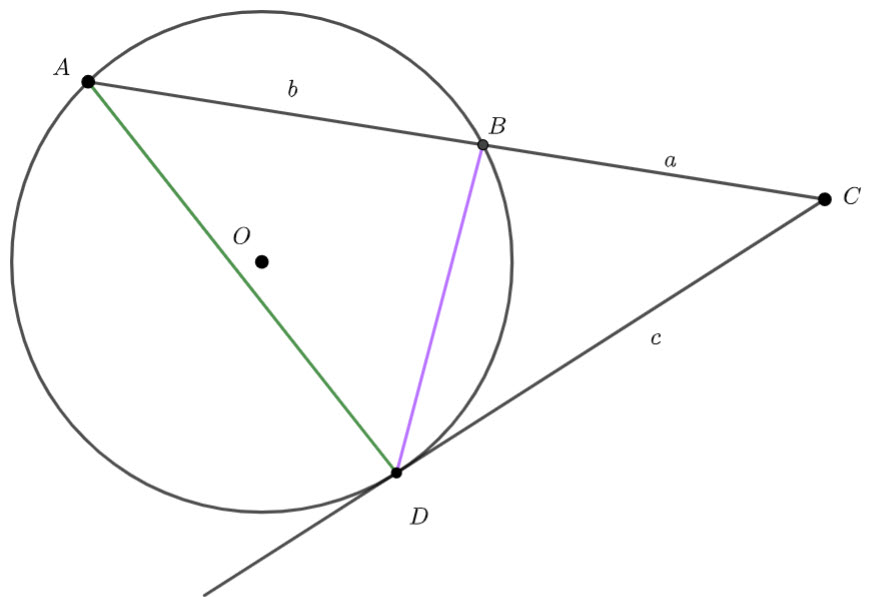
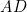 and
and 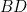 are added
are added![]() (angles in alternate segments are congruent)
(angles in alternate segments are congruent)
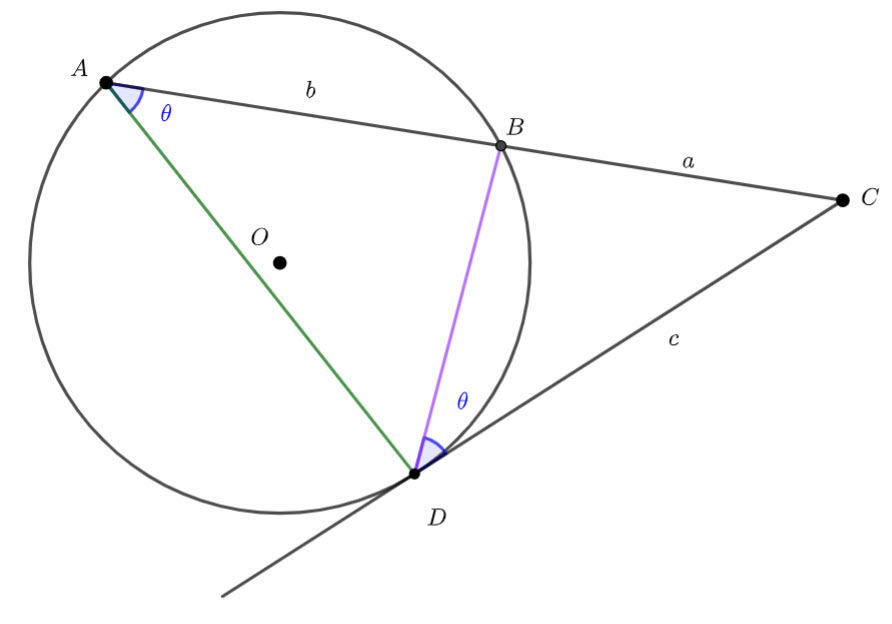
![]() (shared angle)
(shared angle)
![]() (AA)
(AA)
Hence
![]() (Corresponding sides in similar triangles)
(Corresponding sides in similar triangles)
![]()
![]()

Pingback: Circle Geometry Question 2 | Racquel Sanderson