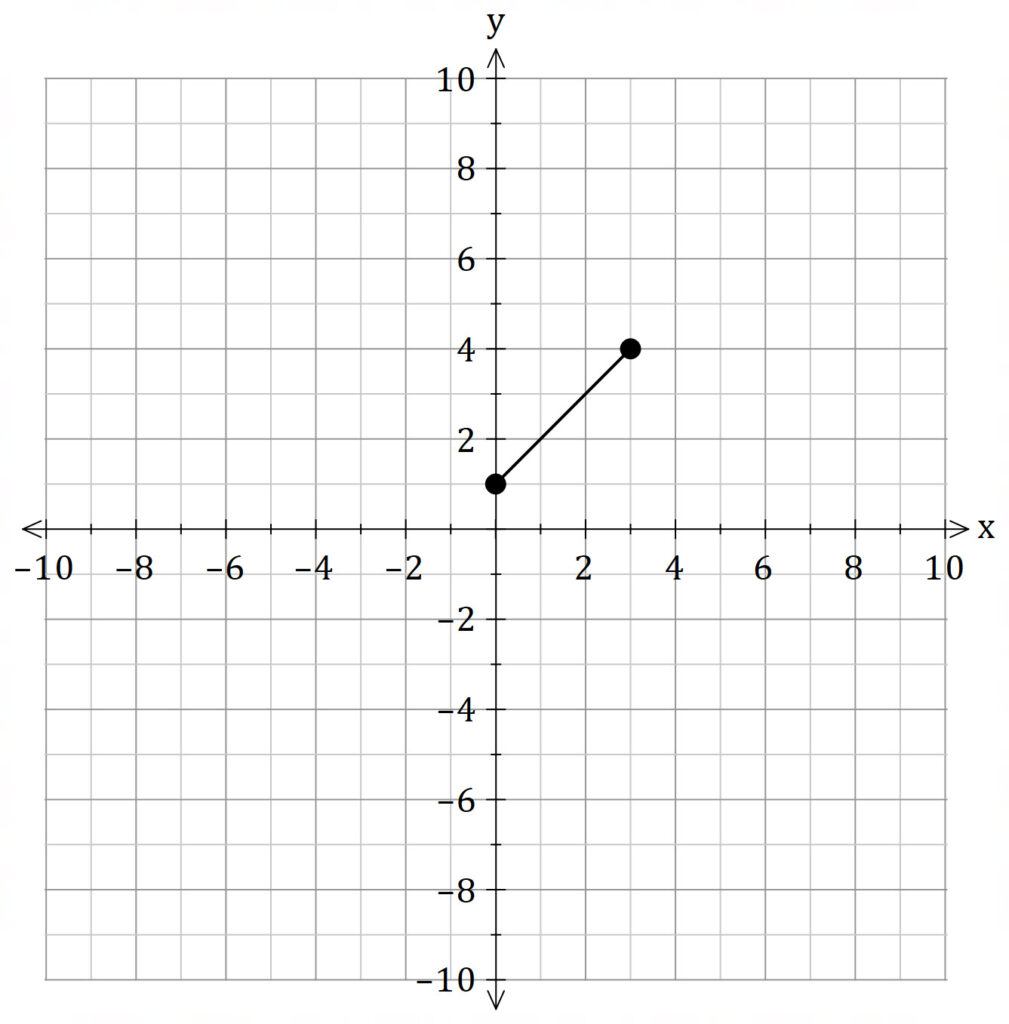
If we rotate this line segment around the ![]() axis, we generate a three dimensional solid.
axis, we generate a three dimensional solid.
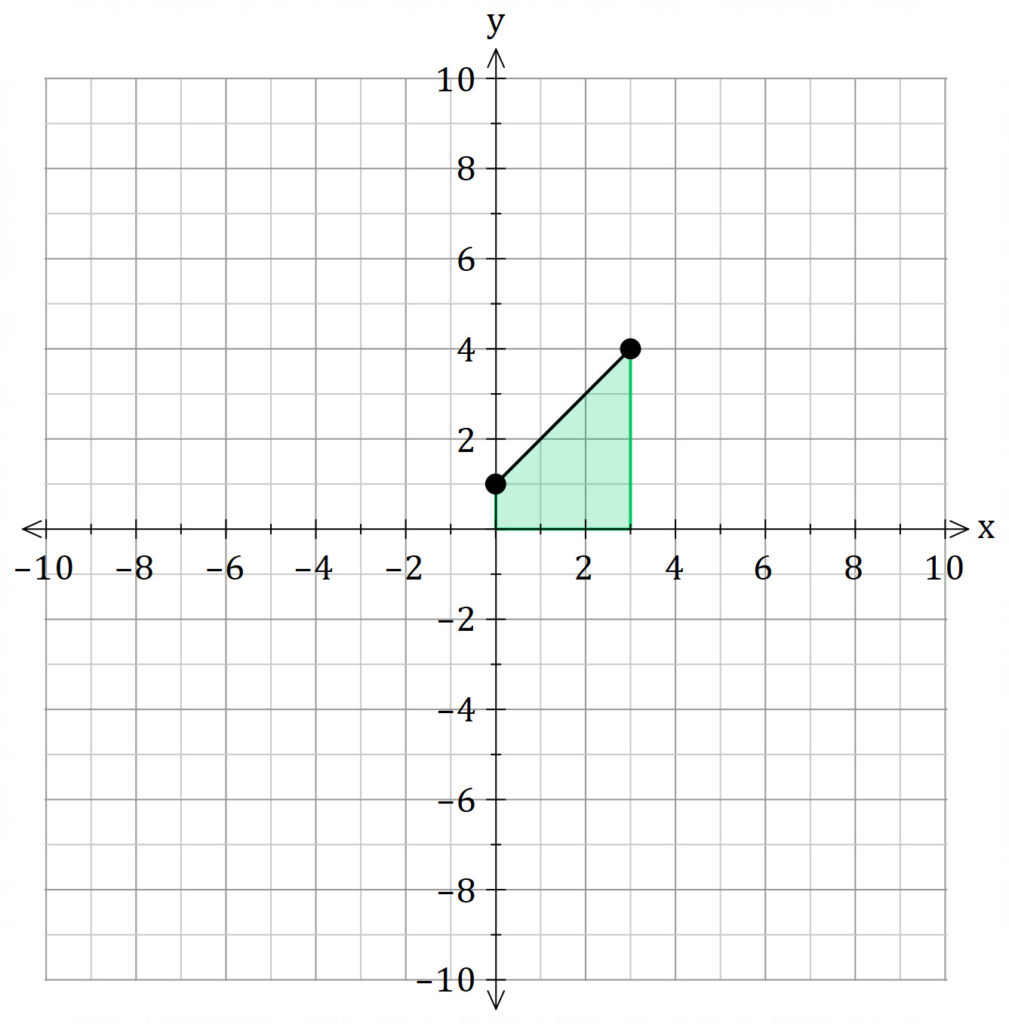
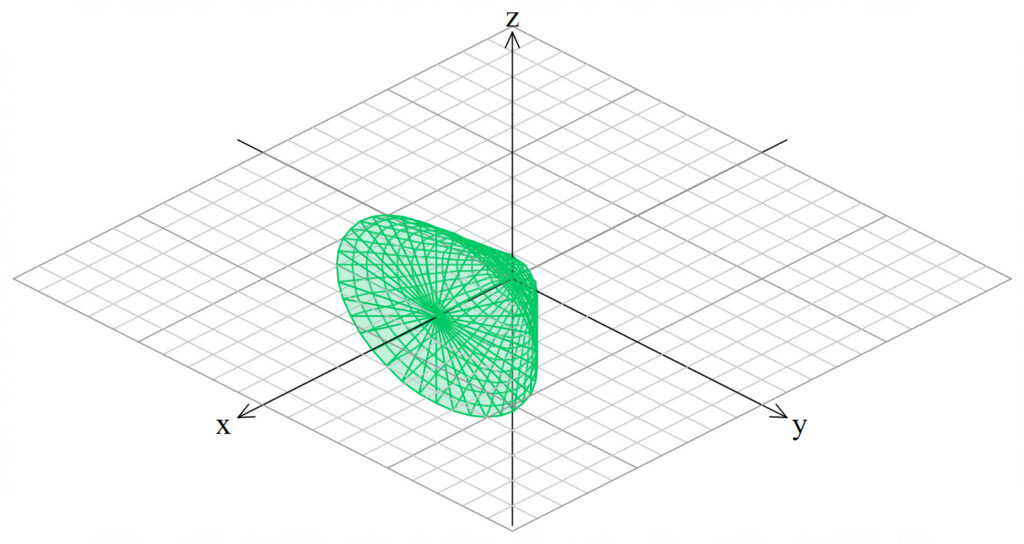
We are going to find the volume of this solid.
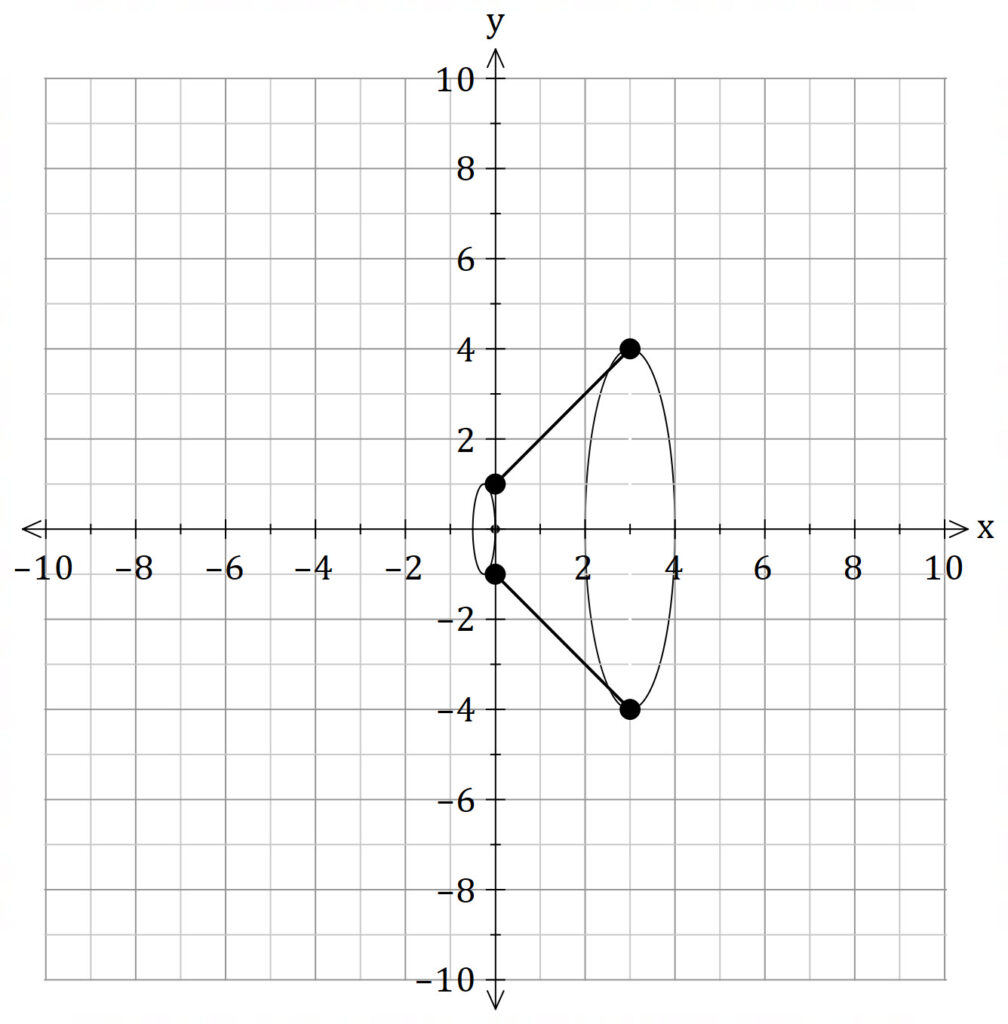
Consider a small section of the line segment and rotate this about the ![]() axis.
axis.
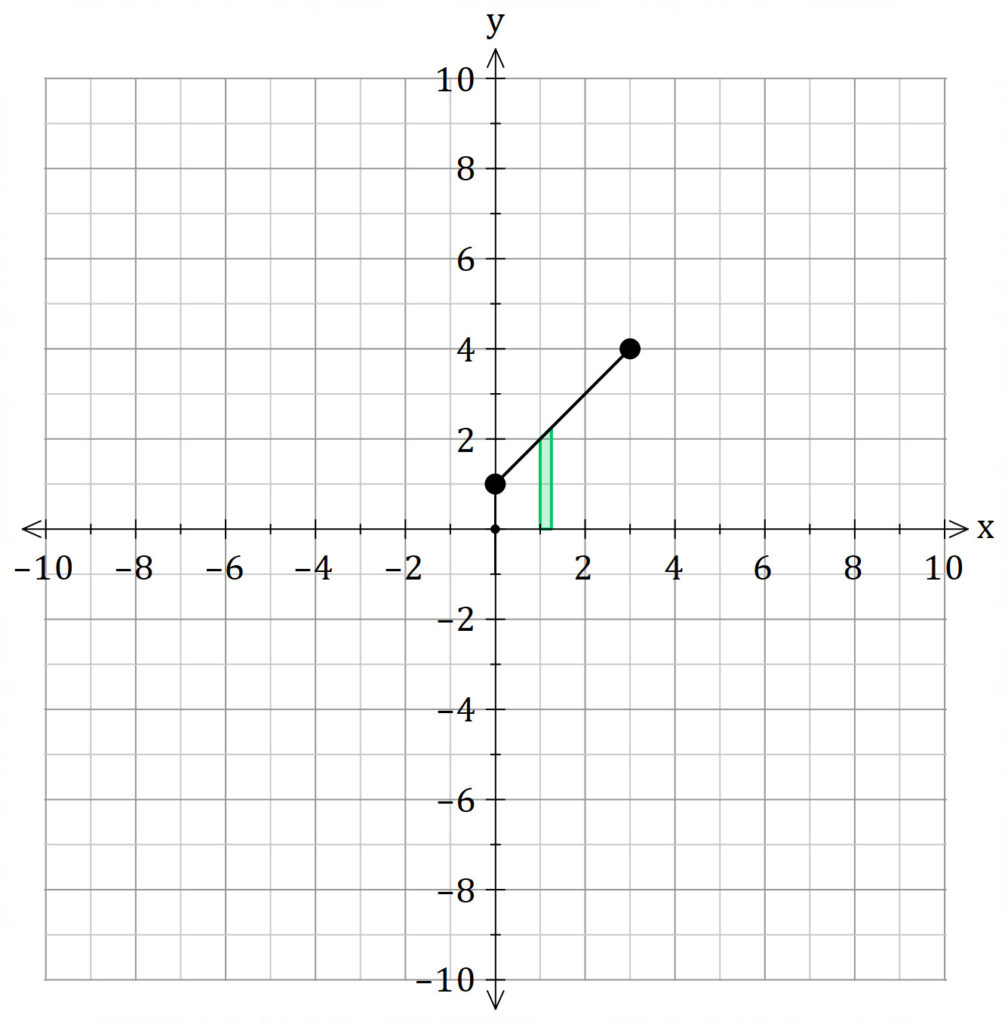
As the width of the section ![]() gets smaller (i.e.
gets smaller (i.e. ![]() ), the solid is a cylinder.
), the solid is a cylinder.
The radius of the cylinder is ![]() and the height of the cylinder is
and the height of the cylinder is ![]() .
.
The volume of a cylinder is ![]()
Hence the volume of our section is
![]()
If we divide our line segment into a large number of cylinders (of equal height) then,
![]()
where ![]() is the lower
is the lower ![]() value and
value and ![]() the upper.
the upper.
Now we want ![]() so
so ![]()
Which is
![]()
Example
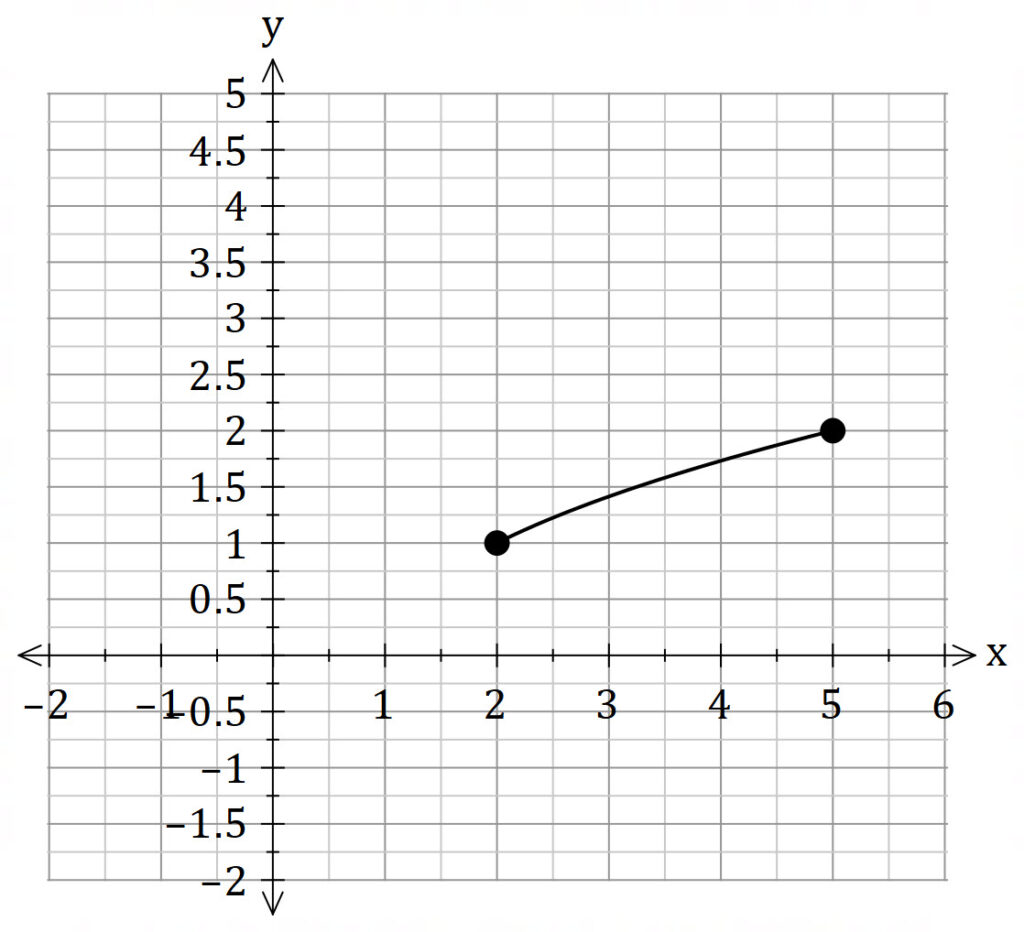
The curve ![]() , where
, where ![]() is rotated about the
is rotated about the ![]() axis to form a solid of revolution. Find the volume of this solid.
axis to form a solid of revolution. Find the volume of this solid.
![]()
![]()
![]()
![]()
![]()

Pingback: Volume of Revolution Method Two (Shell Method) | Racquel Sanderson