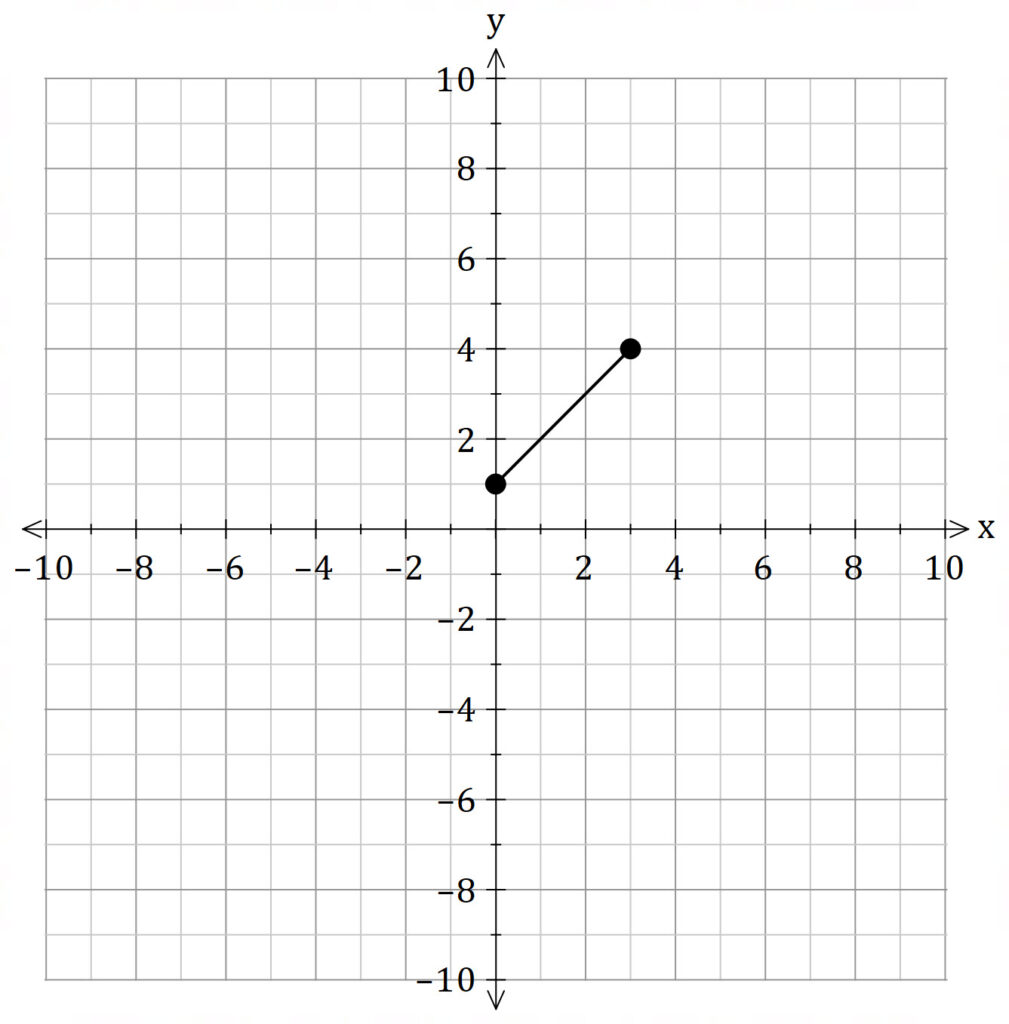
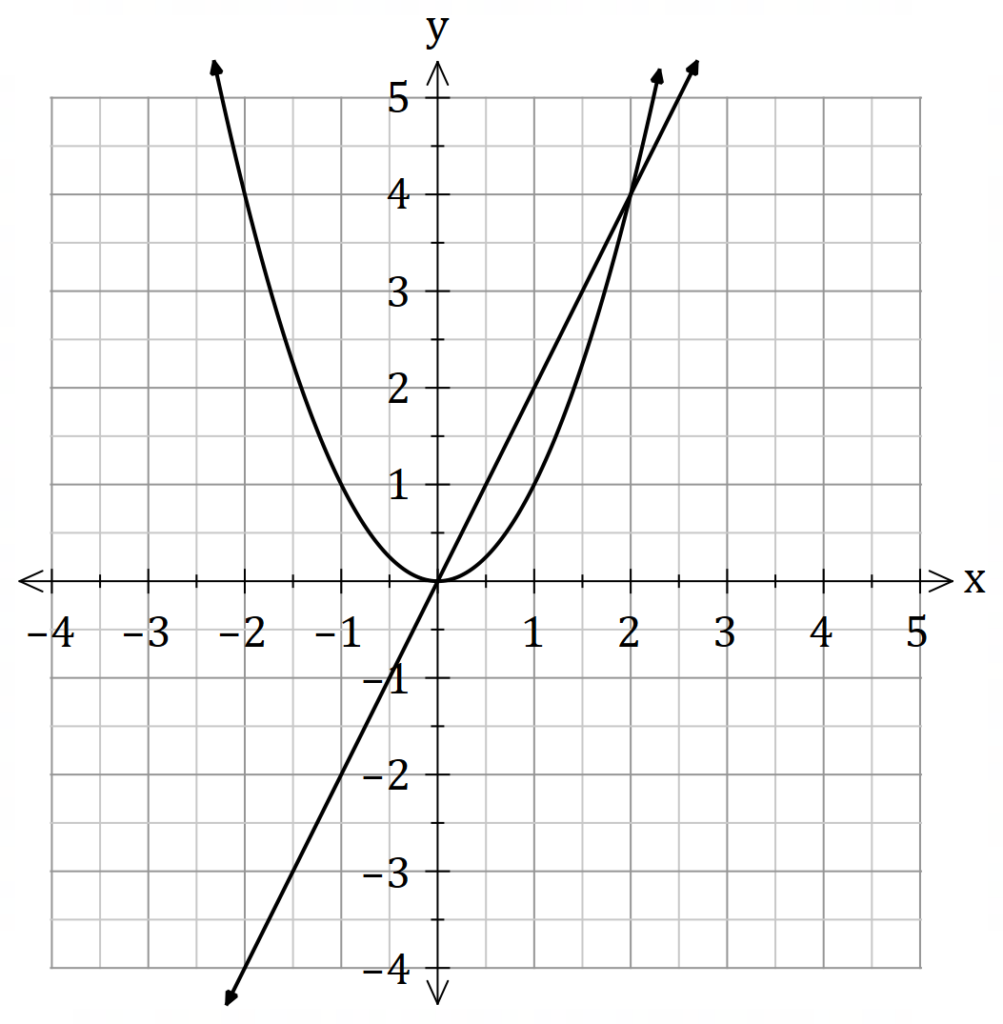
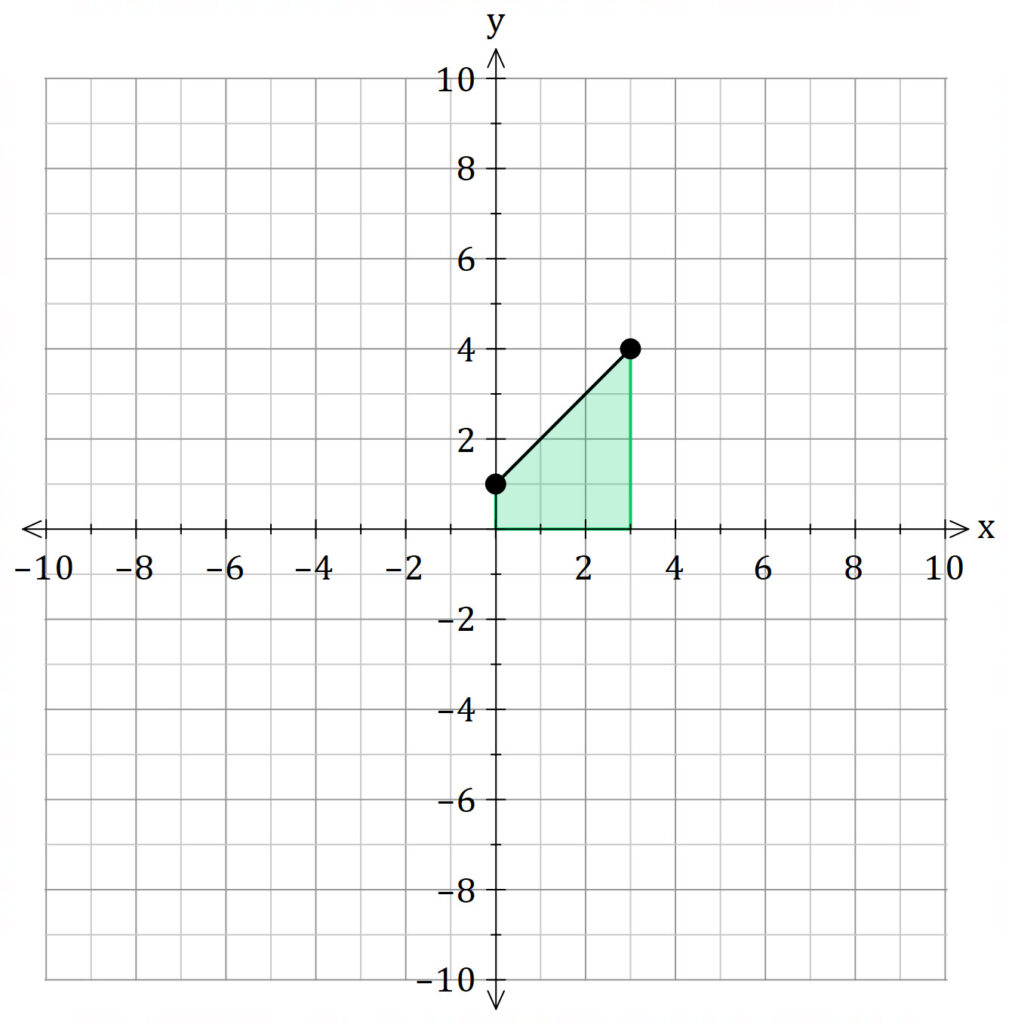
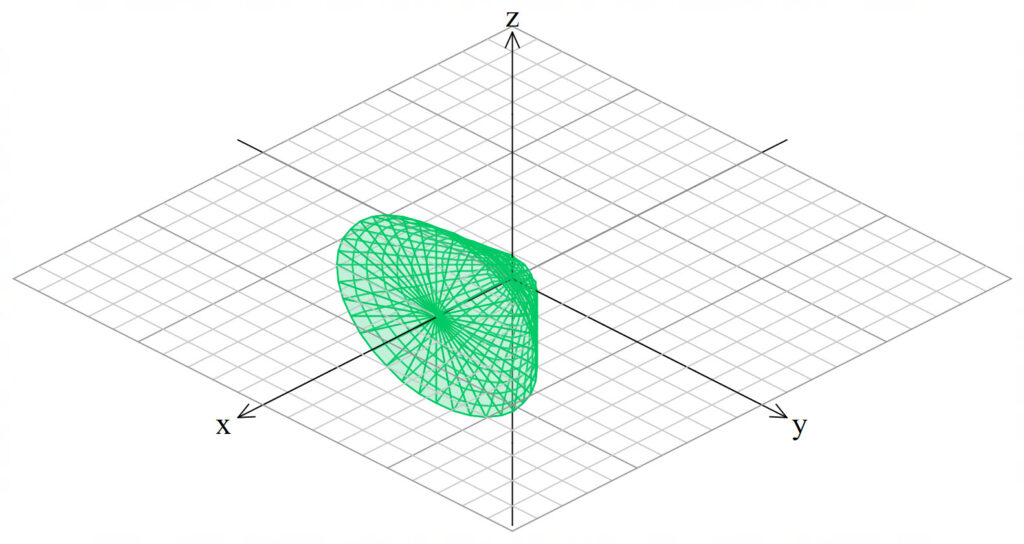
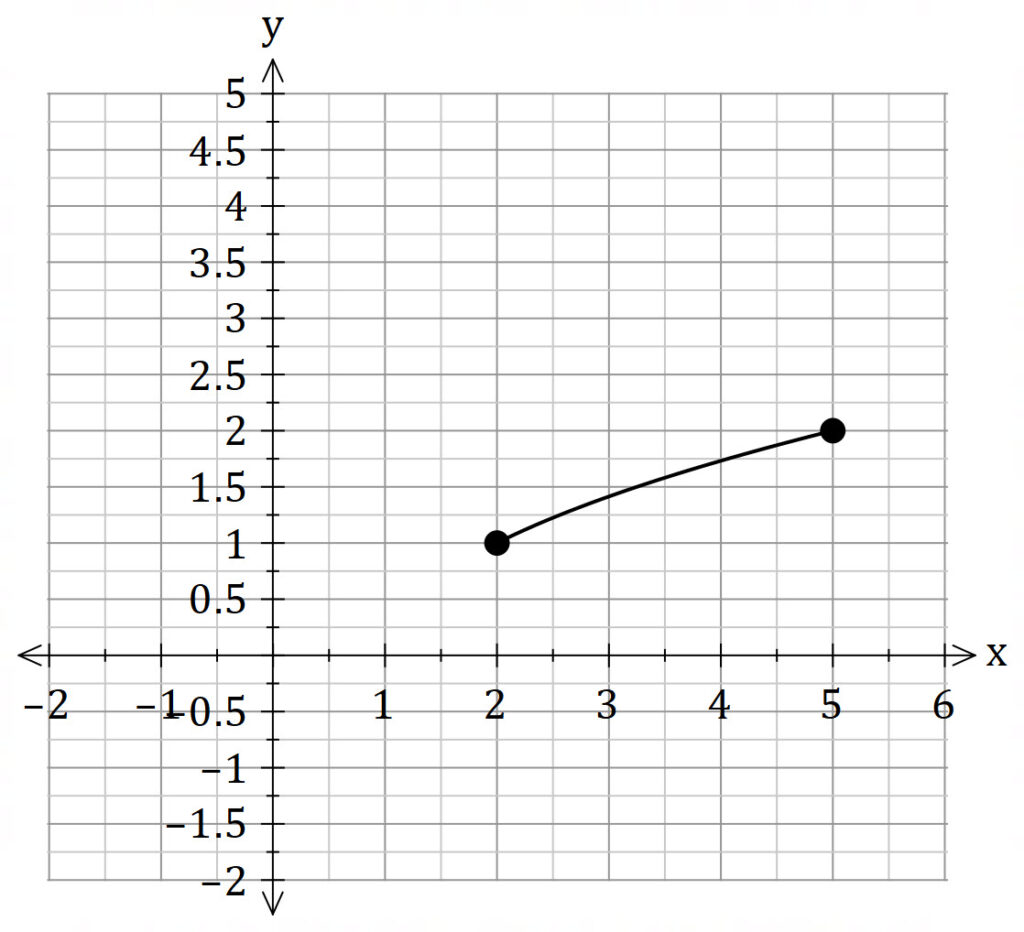
Find the volume of the solid of revolution obtained by rotating the region bounded by
about the line
.
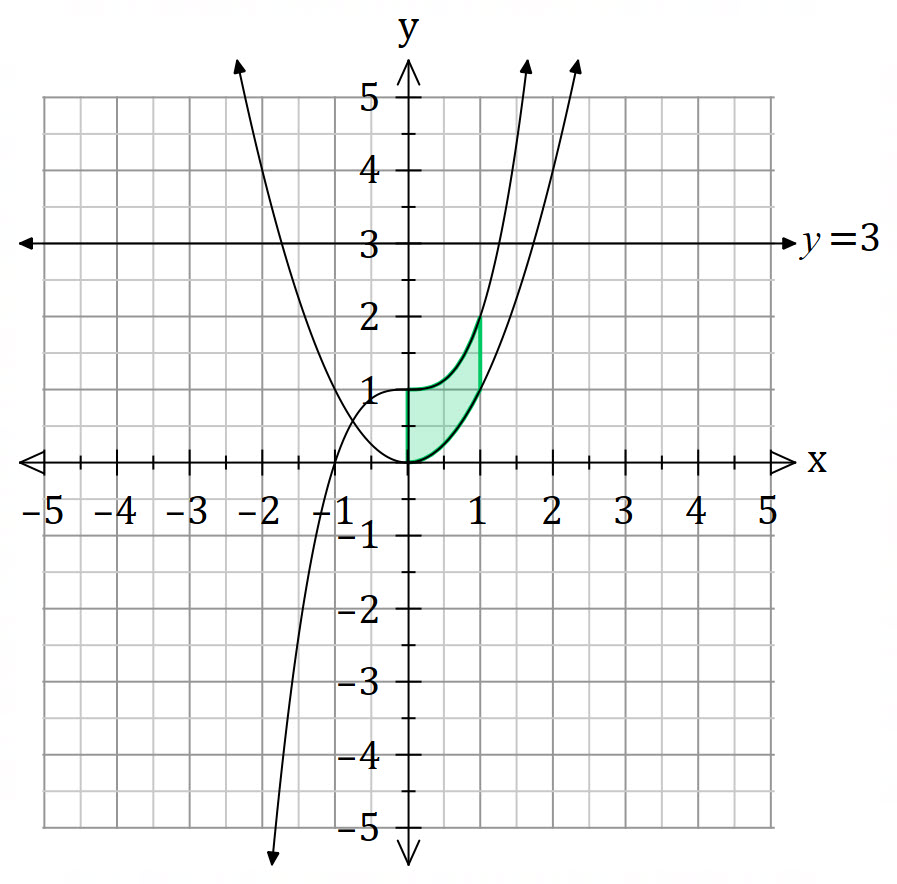
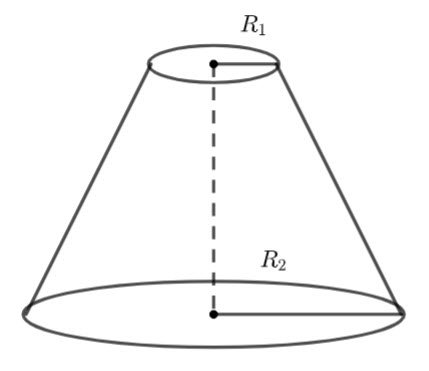
Washer Method
![]()
The volume of the solid is the volume of ![]() rotated about
rotated about ![]() subtract the volume of
subtract the volume of ![]() rotated about
rotated about ![]() .
.
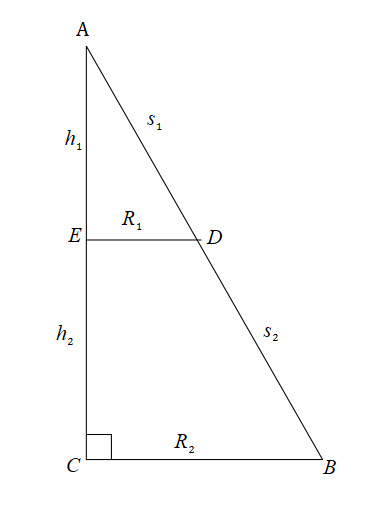
![]()
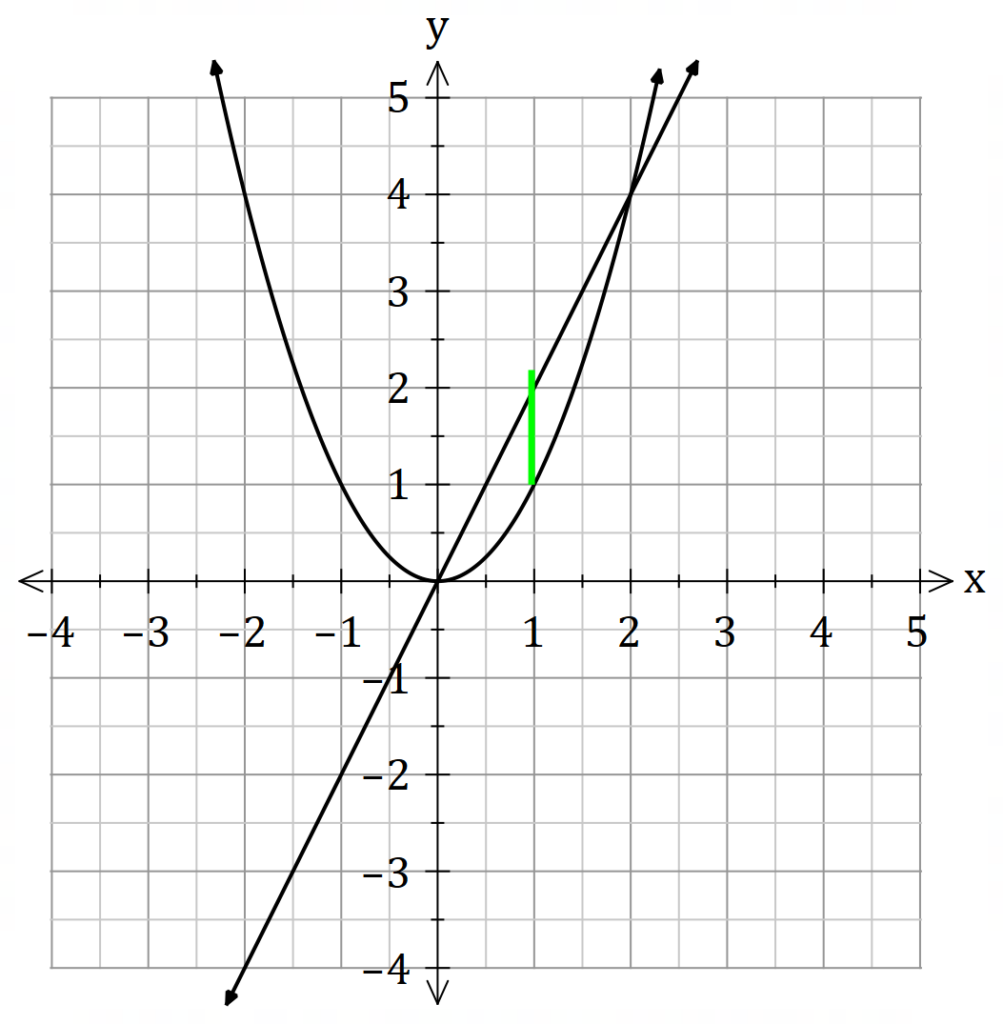
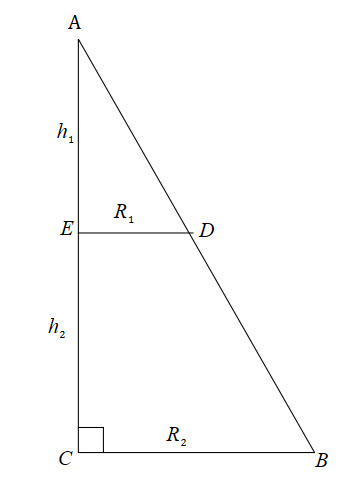
![]() is the distance (i.e radius) of the curve and the line.
is the distance (i.e radius) of the curve and the line.
![]()
![]()
![]()
![]()
![]()
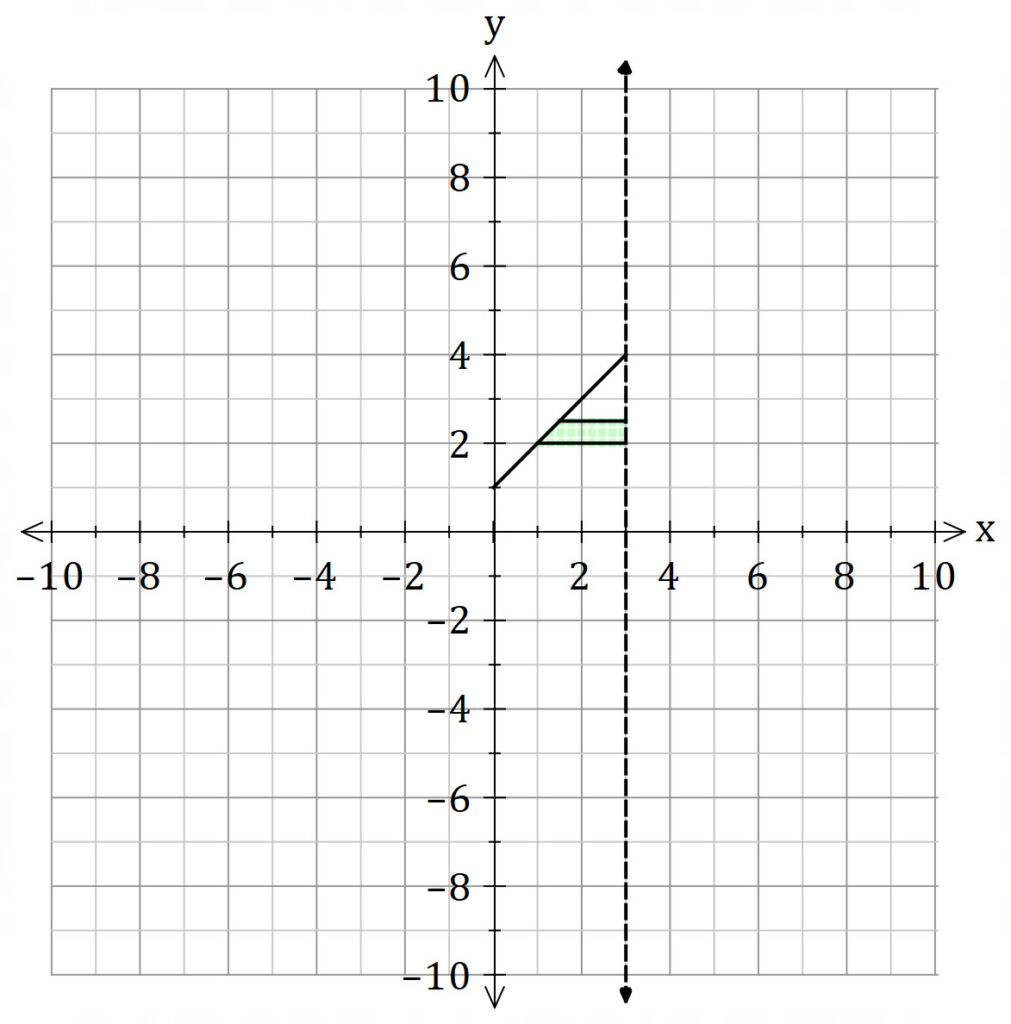
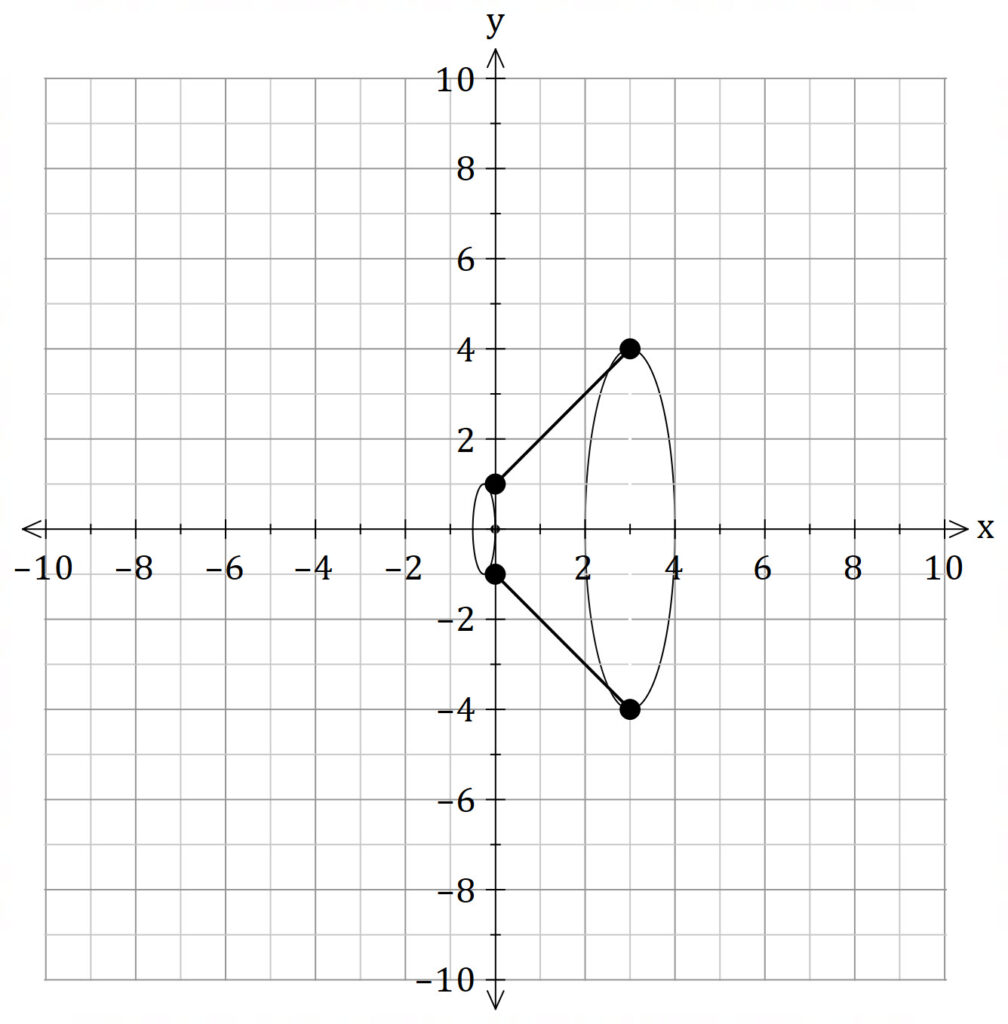
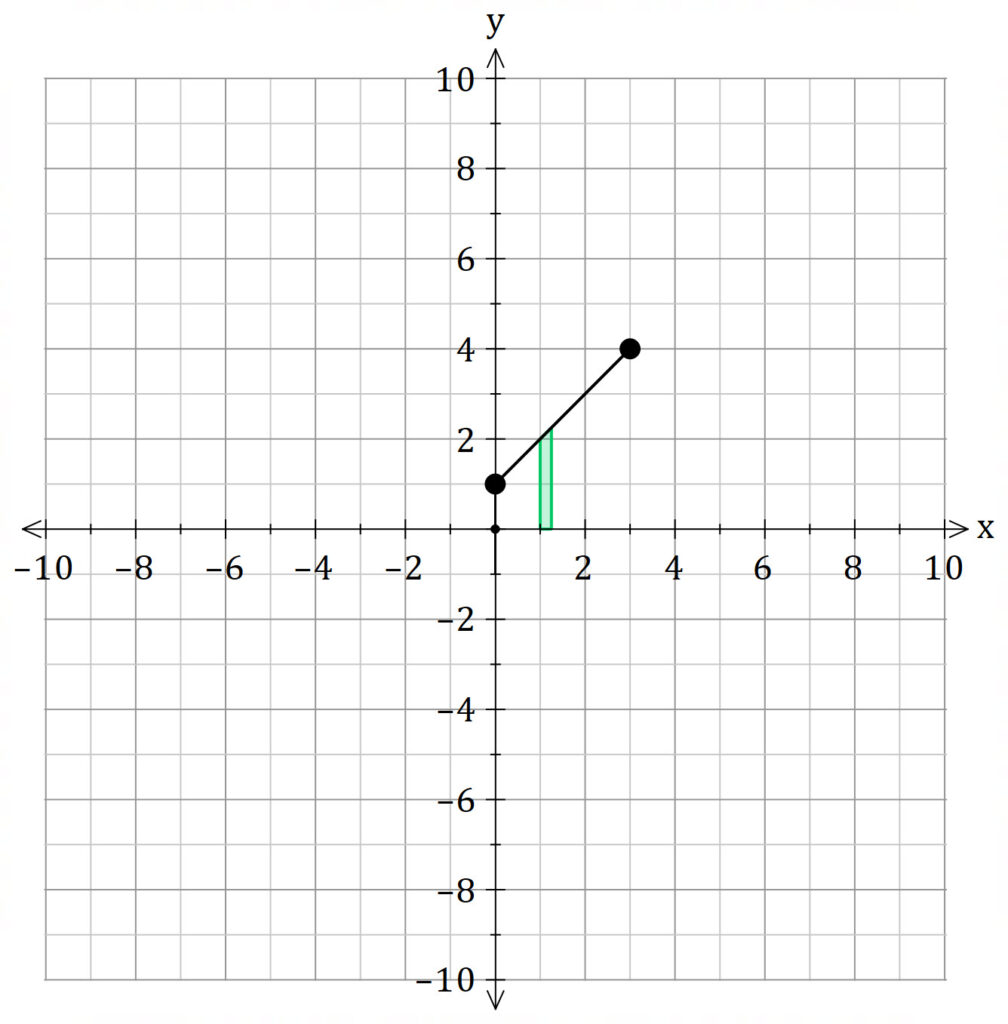
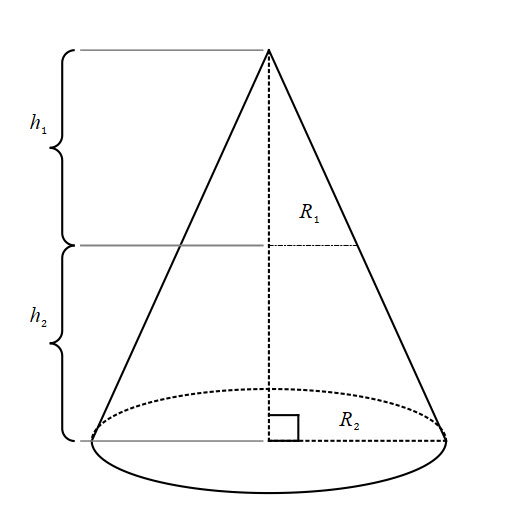
Shell Method
The shell method is much harder because we need to split the integral into two parts.
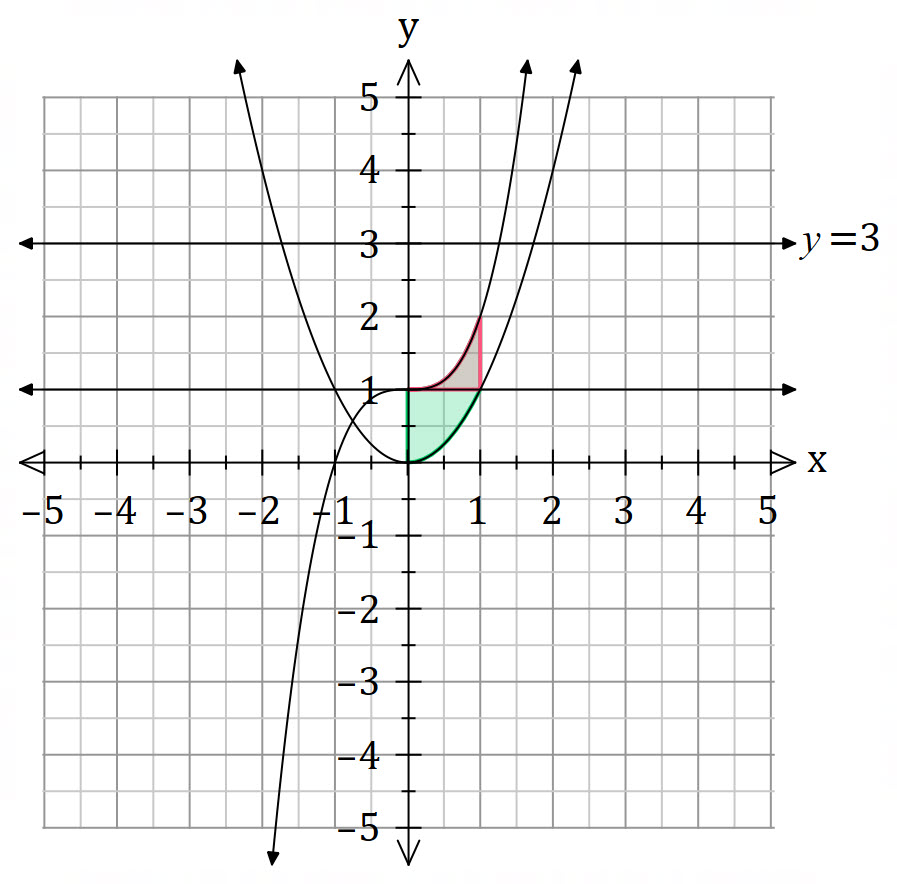
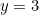 and the red region
and the red region ![]()
![]()
![]() is the distance between each
is the distance between each ![]() value and the line of rotation. For example, if we were rotating about the
value and the line of rotation. For example, if we were rotating about the ![]() axis, the distance is
axis, the distance is ![]() .
.
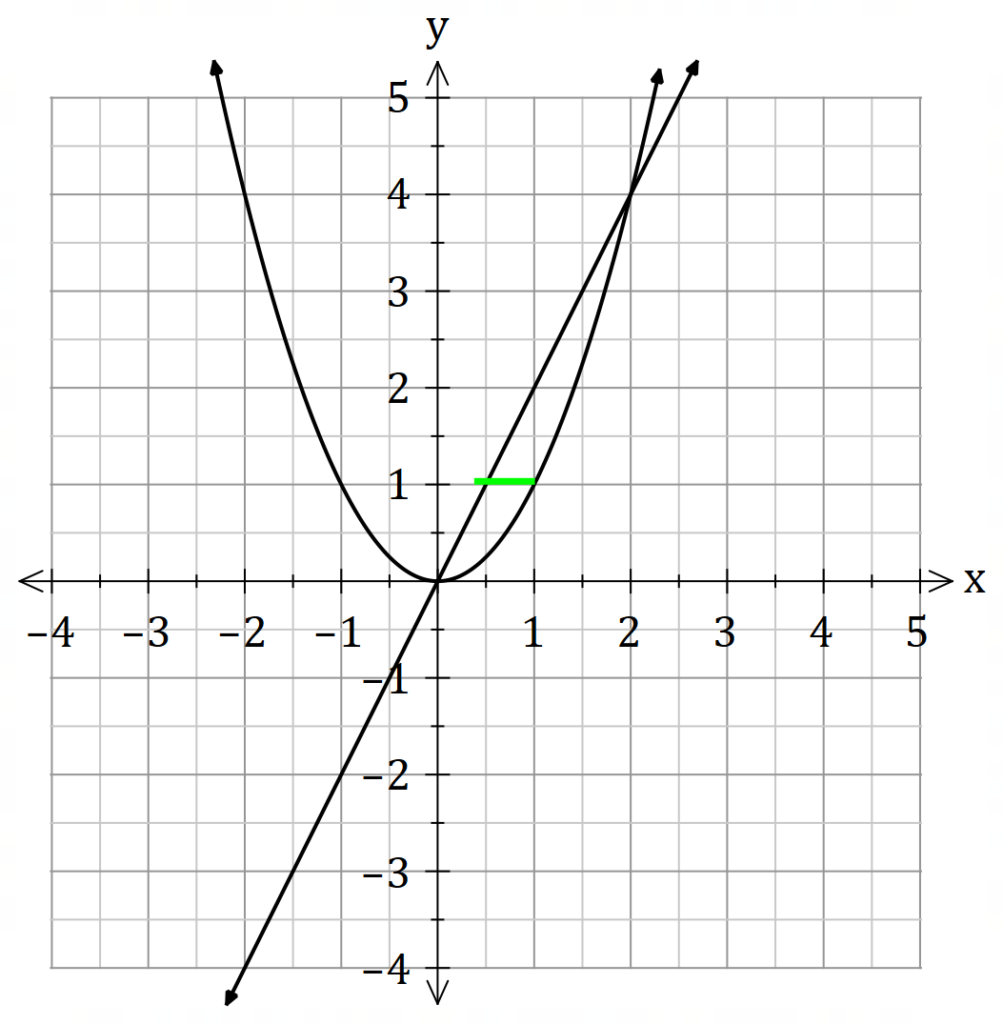
![]() is the height of the cylinder between
is the height of the cylinder between ![]() and
and ![]() .
. ![]() is the height of the cylinder between
is the height of the cylinder between ![]() and
and ![]() . Refer back to Shell method for more information.
. Refer back to Shell method for more information.
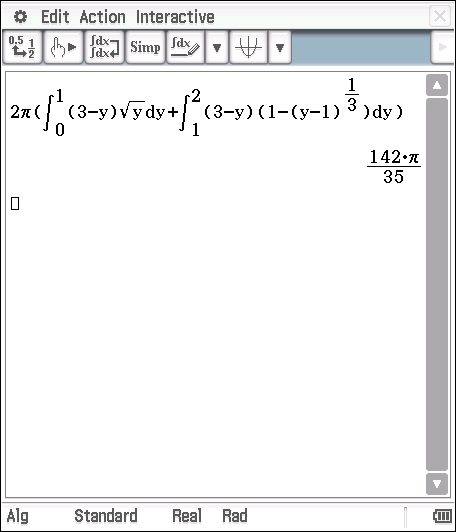
I used a calculator to find this integral