I think this one is doing the rounds, I first saw it here.
![]()
![]() is the obvious answer,
is the obvious answer, ![]() , but are there more answers?
, but are there more answers?
This was my approach
![]()
![]()
![]()
![]()
A quadratic equation.
Hence,
![]()
I then used my calculator
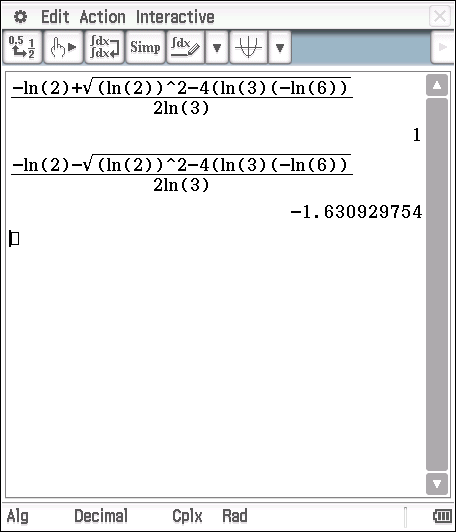
Hence ![]() 0r
0r ![]()
I think this one is doing the rounds, I first saw it here.
![]()
![]() is the obvious answer,
is the obvious answer, ![]() , but are there more answers?
, but are there more answers?
This was my approach
![]()
![]()
![]()
![]()
A quadratic equation.
Hence,
![]()
I then used my calculator

Hence ![]() 0r
0r ![]()
Filed under Algebra, Index Laws, Interesting Mathematics, Quadratics, Solving
Remember
(1) ![]()
We know that ![]() for odd integer multiples of
for odd integer multiples of ![]() , i.e.
, i.e. ![]() , which is
, which is ![]() for
for ![]()
Hence,
![]()
for ![]()
We can factorise our ![]() expansion
expansion
![]()
We know ![]()
![]()
![]()
![]()
I went down a rabbit hole while reading An Imaginary Tale by Paul J Nahin and I decided I wanted to do this…
![]()
![]()
The power series expansion of ![]() is
is
![]()
![]()
![]()
Hence ![]()
![]()
Let’s consider the integral
(1) ![]()
Let ![]() then
then ![]() and
and ![]() where
where ![]()
When ![]() and when
and when ![]()
(2) ![]()
(3) ![]()
Integrate by parts using the tabular method.
| Sign | Differentiate | Integrate |
| + | ||
| – | ||
| + | ||
| – | ||
| + | ||
When we substitute ![]() or
or ![]() the differentiation column is zero except for
the differentiation column is zero except for ![]() , which is
, which is ![]() ,
,
Thus ![]()
![]()
![]()
Now we just need to think about the sign.
![]()
The integral is now
![]()
So ![]()
Let’s work out some partial sums
![]()
Filed under Definite, Integration, Integration by Parts, Tabular Integration
(1) ![]()
I am going to do this integral in two ways; the traditional method and the tabular method.
Traditional Method
Remember ![]()
Let ![]() and
and ![]()
Then ![]() and
and ![]()
![]()
Now we need to do integration by parts on ![]()
Let ![]() and
and ![]()
Then ![]() and
and ![]()
![]()
![]()
![]()
![]()
Tabular Integration
Similar to before, select a ![]() and a
and a ![]() ,
, ![]() and
and ![]()
| Sign | D(ifferentiate) | I(ntegrate) |
| + | ||
| – | ||
| + | ||
| – |
Stop when the differentiating column reaches zero.
Then we multiply diagonally
![]()
![]()
![]()
![]()
It is only worth using this method if integration by parts is required more than once. Also, the ![]() has to eventually differentiate to
has to eventually differentiate to ![]() .
.
Let’s try another one
(2) ![]()
Let ![]() and
and ![]()
| Sign | D | I |
| + | ||
| – | ||
| + | ||
| – | ||
| + |
![]()
![]()
Filed under Integration, Integration by Parts, Tabular Integration
At 10am, object
travelling with constant velocity
km/h is sighted at the point with position vector
km. At 11am object
travelling with constant velocity
km/h is sighted at the point with position vector
km respectively. Use a scalar product method to determine
given that the two objects were closest together at a distance of
km at 4pm.
OT Lee Mathematics Specialist Year 11
At 4pm ![]() is at the point with position vector
is at the point with position vector ![]()
and ![]() is at the point with position vector
is at the point with position vector ![]()
We know the distance between ![]() and
and ![]() at 4pm is
at 4pm is ![]() km.
km.
Hence,
![]()
![]()
![]()
(1) ![]()
In the diagram below, I have found the position vector of ![]() relative to
relative to ![]()
![]() and the velocity of
and the velocity of ![]() relative to
relative to ![]()
![]()
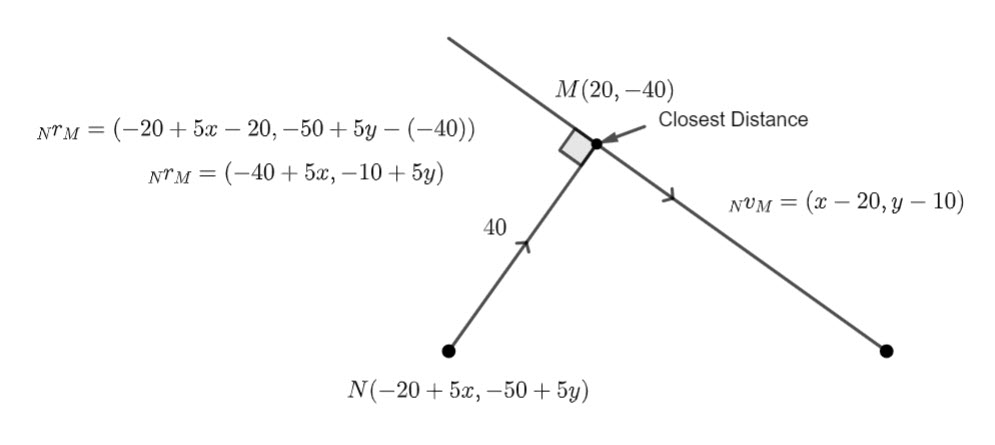
We know that when ![]()
![]() and
and ![]() are the closest distance apart.
are the closest distance apart.
![]()
![]()
![]()
(2) ![]()
Two equations and two unknowns which we can solve simultaneously. Both equations are circles.
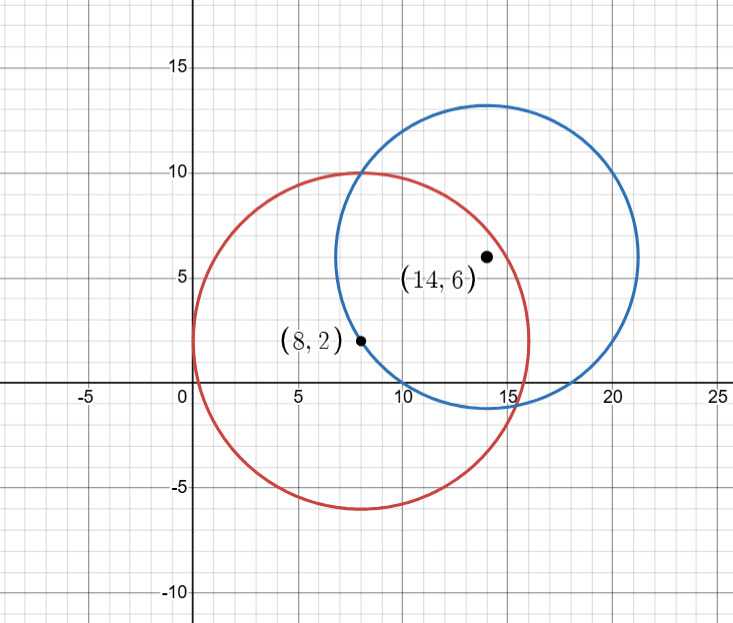
Equation ![]() becomes
becomes
(3) ![]()
and equation ![]() becomes
becomes
(4) ![]()
From equation ![]()
![]()
We will worry about the negative version later.
Substitute for ![]() into equation
into equation ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Square both sides of the equation
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(5) ![]()
Substitute ![]() into
into ![]()
![]()
(6) ![]()
Substitute ![]() into
into ![]()
![]()
(7) ![]()
Now we need to consider the negative version of ![]() . If you work through (like I did above) you end with the same equation for
. If you work through (like I did above) you end with the same equation for ![]() .
.
Hence our two values for ![]() are
are ![]() or
or ![]() .
.
Would someone be expected to do this in an exam? I hope not, but I think its worth doing.
Filed under Closest Approach, Vectors, Year 11 Specialist Mathematics
Sequences are part of the Year 12 Mathematics Applications course and sometimes it’s tricky to work out which terms the question requires.
For example, ATAR 2020 Question 11
Judith monitors the water quality in her garden pond at the same time everyday. She likes to maintain the concentration of algae between 200 and 250 unites per 100 litres (L). Her measurements show that the concentration increases daily according to the recursive rule
where
units per 100 L (the minimum concentration)
When the concentration gets above the 250 units per 100 L limit, she treats the water to bring the concentration back to the minimum 200 units per 100 l.
(a) If Judith treated the water on Sunday 6 December 2020, determine
(i) the concentration on Wednesday, 9 December 2020.
(ii) the day when she next treated the water.(b) During the first week of January 2021, Judith monitored the water and recorded the following readings
| Day | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Concentration (C) | 200 | 206 | 212.28 | 218.55 | 225.10 | 231.85 | 238.81 |
(i) Determine the revised recursive rule.
(ii) If she treated the water on 10 January and went on holiday until 20 January, when she next treated the water, calculate the concentration of the water on her return. Assuming the recursive rule from (b)(i) is used.
| (a)(i) If I find most students simply do It’s better to list them 6th 7th 8th 9th Hence we want to find The concentration on Wednesday 9 December is 215.38 units per 100 L a(ii) We need to find when the concentration is greater than 250 The 9th is Judith next treats the water on Wednesday 16 December (b) (i) (ii) The concentration of the water on Judith’s return is 268.78 units per 100 L |
I get my students to count on their fingers to ensure they get the correct term or day.
My year 12 Mathematical Methods students have questions like this
Given that
is continuous everywhere and that
, find:
(a)
(b)
(c)
(d)
(e)
(f)
OT Lee Mathematics Methods Textbook Ex 8.3 question 6
For the most part these questions aren’t too difficult, but the horizontal dilations cause issues.
| (a) (b) (c) Let When (d) Let When (e) Let When (f) Let When | Split the integral Integrate the first part. This is a horizontal translation (one unit to the right) so the shape of the curve doesn’t change. The integration bounds have also shifted one unit to the right. This is a horizontal dilation and translation. The easiest method is to use a change of variable |
Once you get the hang of it, you can skip the change of variable and multiply the value of the definite integral by the scale factor of the horizontal dilation (only if the integration bounds are also changed).
Filed under Definite, Integration, Uncategorized, Year 12 Mathematical Methods