The following question is from the 2019 ATAR Mathematics Applications Paper – Calculator Free Question 3.
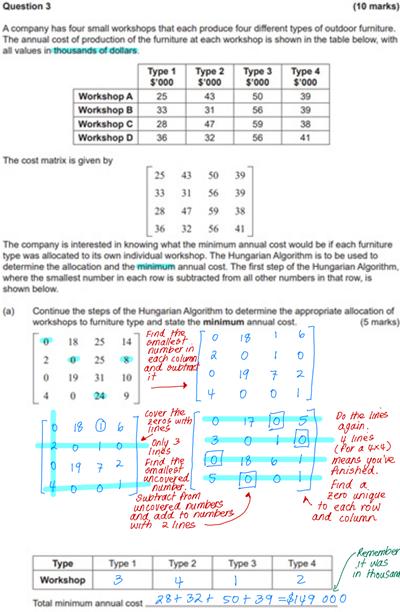

The following question is from the 2019 ATAR Mathematics Applications Paper – Calculator Free Question 3.


Filed under Networks, Year 12 Mathematics Applications
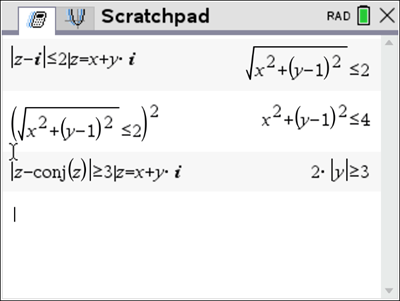
Let ![]() be the region of the complex plane where the inequalities
be the region of the complex plane where the inequalities ![]() and
and ![]() hold simultaneously.
hold simultaneously.
First find the Cartesian equations.
Finding the symbols The Menu – Number – Complex Number Tools – Complex Conjugate  |
Second, sketch each of the functions.
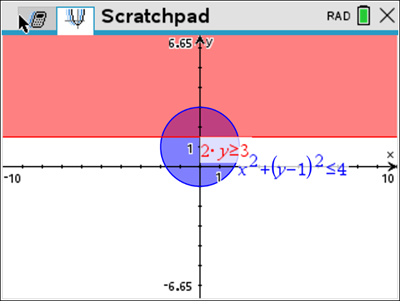
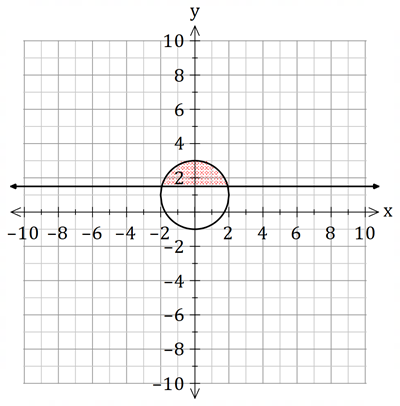
The section that is shaded twice is our region.
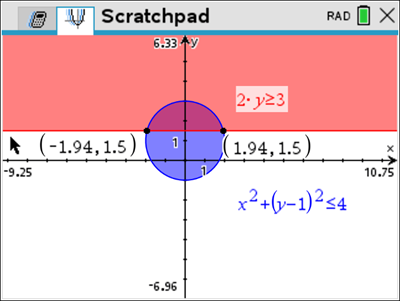
Determine the minimum value of ![]() in
in ![]() .
.
We can find the point of intersection between the circle and the line.
![]()
Or if you want exact values
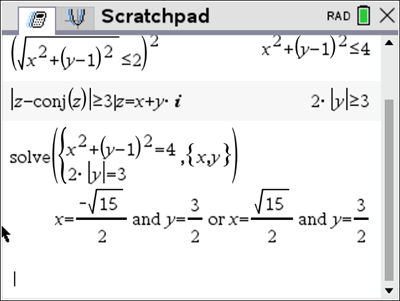
Use the Solve Systems of Equations tool – Menu – Algebra – Solve Systems of Equations – Solve Systems of Equations.
![]()
This was a question one of my year 9s had to tackle:
A hemisphere of radius length 5cm is partially filled with water. The top of the hemisphere is horizontal and the surface of the water is a circle of radius 4cm. Find the depth of the water.
ICE-EM Mathematics 9, page 70, question 2
Below is a cross section of the hemisphere
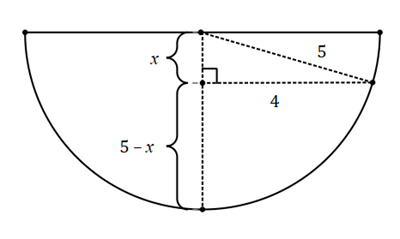
The depth of the water is ![]()
We can find ![]() using the Pythagorean theorem
using the Pythagorean theorem
![]()
![]() (it’s the classic 3-4-5 triangle)
(it’s the classic 3-4-5 triangle)
Hence the depth of the water is 2cm.
Filed under Pythagoras