This is one of those theorems, where the name is probably not the person who discovered it. Check out the Wikipedia entry for more information on the history.
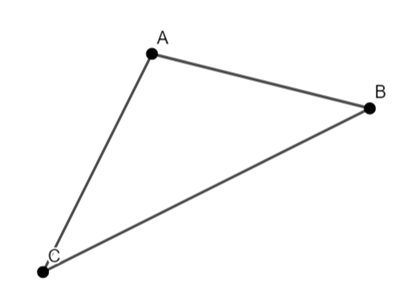
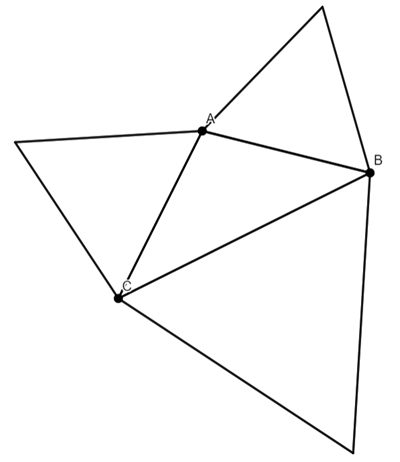
Napoleon’s theorem states that if equilateral triangles are constructed on the sides of any triangle, either all outward or all inward, the lines connecting the centres of those equilateral triangles themselves form an equilateral triangle.
I am just going to look at the outward triangles.
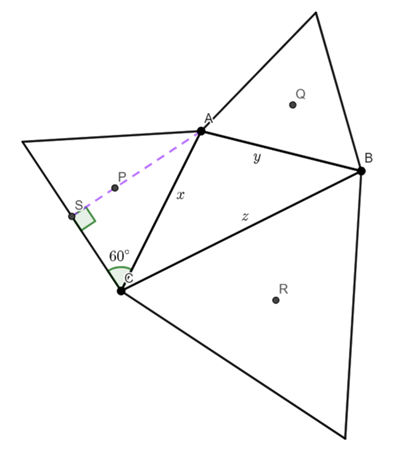
Construct equilateral triangles on the edges AB, BC and AC.
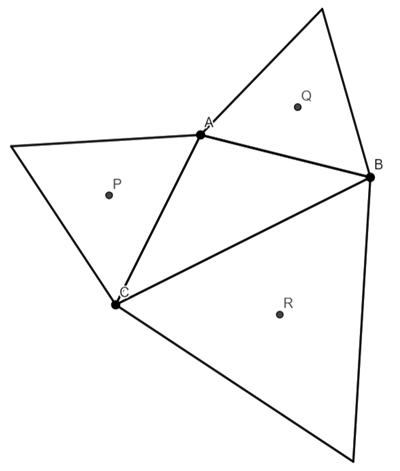
Find the centre (Centroid) of these triangles.
Note: The centroid is the point of intersections of the medians.
A median is the line from a vertex to the midpoint of the opposite side.
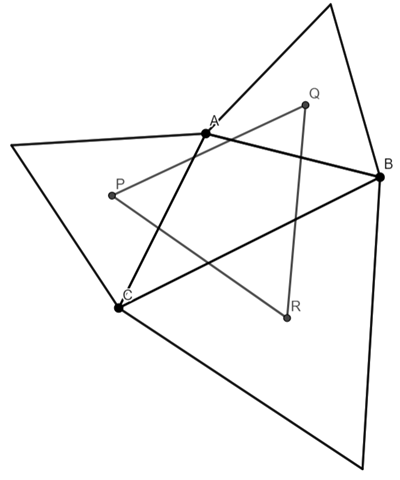
We are going to prove that triangle PQR is equilateral
I am going to add AP, AQ, QB, BR, RC and CP
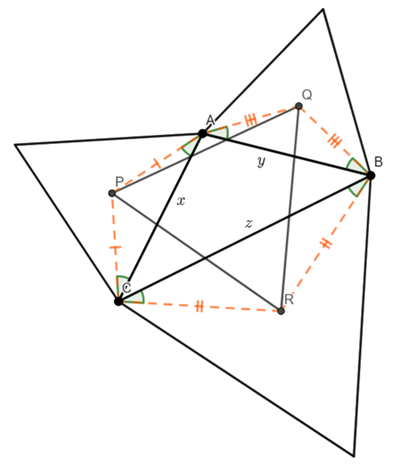
As P, Q and R are the centroids, PA=PC, QA=QB, and RB=RC.
Therefore triangles AQB, BRC, and CPA are isosceles.
The angles QAB, QBA, RBC, RCB, PCA, PAC (the shaded angles in the above diagram) are 30 degrees, because the line bisects the angle (and the angle is 60 degrees because the triangles are equilateral).
Now for the maths.
![Rendered by QuickLaTeX.com \[\textnormal {Let}\ AB=y,\ AC=x,\ BC=z\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-0a202b0f006432d8dd90e8b609d70fc8_l3.png)
![Rendered by QuickLaTeX.com \[\textnormal {Let}\ \angle{CAB}=\theta,\ \angle{ABC}=\alpha,\ \angle{BCA}=\gamma\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-0b06510049efb29f6cd00c6d1ce5111e_l3.png)
![Rendered by QuickLaTeX.com \[\therefore\angle{PAQ}=(60+\theta),\ \angle{QBR}=(60+\alpha),\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-8ea08beb2a901e6510a4a7cdb218921e_l3.png)
![Rendered by QuickLaTeX.com \[ \angle{RCP}=(60+\gamma)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-6e000b656e4509c8368ea5bfed8a0c22_l3.png)
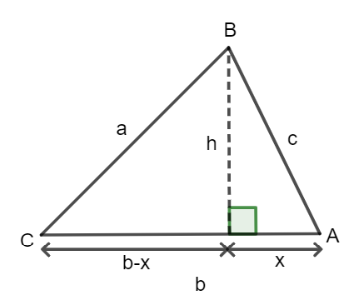
PA is 2/3 the length of the median.
AS is the median
![Rendered by QuickLaTeX.com \[sin(60)=\frac{AS}{x}\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-7939e7d93aab91f09474b42a7aed1ee9_l3.png)
![Rendered by QuickLaTeX.com \[AS=xsin(60)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-e85717e7c3d20af7dd6048f71216a8a4_l3.png)
![Rendered by QuickLaTeX.com \[AS=\frac{\sqrt{3}}{2}x\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-9f21b71acd4008d18c10cb0480e37254_l3.png)
Hence,
![Rendered by QuickLaTeX.com \[PA=\frac{2}{3}\frac{\sqrt3}{2}x\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-9ebc3c9e56fcc11bf885e0a21af9c910_l3.png)
![Rendered by QuickLaTeX.com \[PA=\frac{\sqrt{3}}{3}x\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-d5532ce0c0c81b58b0a919049888e378_l3.png)
![Rendered by QuickLaTeX.com \[PA=\frac{x}{\sqrt{3}}\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-eaed84f2daf0fd839648666b7125b545_l3.png)
In the same manner,
![Rendered by QuickLaTeX.com \[QA=\frac{y}{\sqrt{3}}\ \textnormal {and} \ BR=\frac{z}{\sqrt{3}}\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-ddbfca3228d890b08fa79314d2d68795_l3.png)
Using the cosine rule
![Rendered by QuickLaTeX.com \[(PQ)^2=(\frac{x}{\sqrt{3}})^2+(\frac{y}{\sqrt{3}})^2-2\frac{x}{\sqrt{3}}\frac{y}{\sqrt{3}}cos(60+\theta)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-f30149da2a40f25ac976c813aa11c68f_l3.png)
![Rendered by QuickLaTeX.com \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}cos(60+\theta)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-4091c96b5c5f84a12d6cc264c15695f9_l3.png)
![Rendered by QuickLaTeX.com \[\textnormal{Use a trigonometric identity to expand}\ cos(60+\theta)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-d755c54e37c7a3a26ac1788348b97742_l3.png)
![Rendered by QuickLaTeX.com \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}(cos60cos\theta-sin60sin\theta)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-82401ff7593bb721159a4c87c1b1e0eb_l3.png)
![Rendered by QuickLaTeX.com \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}(\frac{1}{2}cos\theta-\frac{\sqrt{3}}{2}sin\theta)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-eebbbc1c30a6f1b8de7ebd29efef2478_l3.png)
Now from the original triangle ABC
![Rendered by QuickLaTeX.com \[cos\theta=\frac{x^2+y^2-z^2}{2xy}\ \textnormal {and}\ A=\frac{1}{2}xysin\theta\ \textnormal {where} A\ \textnormal {is the area.}\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-0dca65a1cffba41ee639db3e7939c760_l3.png)
![Rendered by QuickLaTeX.com \[\textnormal{Substitute into}\ (PQ)^2 \]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-899e9e8d0156b7cc097208db341d92a9_l3.png)
![Rendered by QuickLaTeX.com \[(PQ)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xy}{3}(\frac{x^2+y^2-z^2}{4xy}-\frac{\sqrt{3}A}{xy})\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-9ec10ee252942c31b363a6b22a0af68e_l3.png)
Multiply both sides by 3 and expand and simplify
![Rendered by QuickLaTeX.com \[3(PQ)^2=x^2+y^2-2xy(\frac{x^2+y^2-z^2}{4xy}-\frac{\sqrt{3}A}{xy})\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-3163ed2ffe449e6026a29ba65c43d931_l3.png)
![Rendered by QuickLaTeX.com \[3(PQ)^2=x^2+y^2-(\frac{x^2}{2}+\frac{y^2}{2}-\frac{z^2}{2}-2\sqrt{3}A)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-2673582b21222e561491591220bbcef2_l3.png)
![Rendered by QuickLaTeX.com \[3(PQ)^2=\frac{x^2}{2}+\frac{y^2}{2}+\frac{z^2}{2}+2\sqrt{3}A\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-c61f620ffa9bf574dd3b8fd721ea238d_l3.png)
We are going to do the same for QR
![Rendered by QuickLaTeX.com \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2yz}{3}(cos(60+\alpha)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-980d3939635271aa1be3e1e48d26a4c5_l3.png)
![Rendered by QuickLaTeX.com \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2xy}{3}(cos60cos\alpha-sin60sin\alpha)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-22accfd85f62082d882a189f2698e0a1_l3.png)
![Rendered by QuickLaTeX.com \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2xy}{3}(\frac{1}{2}cos\alpha-\frac{\sqrt{3}}{2}sin\alpha)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-a3b50d9361acd0cb739c35bf8876a2f8_l3.png)
Once again, from triangle ABC
![Rendered by QuickLaTeX.com \[cos\alpha=\frac{y^2+z^2-x^2}{2yz}\ \textnormal {and}\ A=\frac{1}{2}zysin\alpha\ \textnormal {where} A\ \textnormal {is the area.}\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-cdb8478ab8c4542a9f35306c3dfaaae9_l3.png)
![Rendered by QuickLaTeX.com \[\textnormal{Substitute into}\ (QR)^2 \]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-ae91f673de38b6758bf68e0ba73020cd_l3.png)
![Rendered by QuickLaTeX.com \[(QR)^2=\frac{y^2}{3}+\frac{z^2}{3}-\frac{2yz}{3}(\frac{y^2+z^2-x^2}{4yz}-\frac{\sqrt{3}A}{yz})\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-b9c434214e372e86b08ca08595604154_l3.png)
Multiply both sides by three and expand and simplify
![Rendered by QuickLaTeX.com \[3(QR)^2=y^2+z^2-2yz(\frac{y^2+z^2-x^2}{4yz}-\frac{\sqrt{3}A}{yz})\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-371a3e0e0eb364d0feeebca906eba8b5_l3.png)
![Rendered by QuickLaTeX.com \[3(QR)^2=y^2+z^2-(\frac{y^2}{2}+\frac{z^2}{2}-\frac{x^2}{2}-2\sqrt{3}A)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-eb418d45e98aa8e35ca003ad5d29c2c4_l3.png)
![Rendered by QuickLaTeX.com \[3(QR)^2=\frac{x^2}{2}+\frac{y^2}{2}+\frac{z^2}{2}+2\sqrt{3}A\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-980d6b131deb8abcdef31da91592d680_l3.png)
We can do the same for PR
![Rendered by QuickLaTeX.com \[(PR)^2=\frac{x^2}{3}+\frac{z^2}{3}-\frac{2xz}{3}cos(60+\gamma)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-557df3c5b17eb8e3854b869f5ac21bab_l3.png)
![Rendered by QuickLaTeX.com \[(PR)^2=\frac{x^2}{3}+\frac{z^2}{3}-\frac{2xz}{3}(cos60cos\gamma-sin60sin\gamma)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-3c8d581836622a0abe2a9146ffac9447_l3.png)
![Rendered by QuickLaTeX.com \[(PR)^2=\frac{x^2}{3}+\frac{z^2}{3}-\frac{2xz}{3}(\frac{1}{2}cos\gamma-\frac{\sqrt{3}}{2}sin\gamma)\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-ee3adc1751d812f92148bdecd94f983b_l3.png)
And from triangle ABC
![Rendered by QuickLaTeX.com \[cos\gamma=\frac{x^2+z^2-y^2}{2xz}\ \textnormal{and}\ A=\frac{1}{2}sin\gamma\ \textnormal{where A is the area.}\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-f1d0db90cef404a4d5ec60fd96cea271_l3.png)
![Rendered by QuickLaTeX.com \[\textnormal{substitute into}\ (PR)^2\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-e86755940ae797e2599d1679c8228e7f_l3.png)
![Rendered by QuickLaTeX.com \[(PR)^2=\frac{x^2}{3}+\frac{y^2}{3}-\frac{2xz}{3}(\frac{x^2+z^2-y^2}{4xz}-\frac{\sqrt{3}A}{xz})\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-0bb74378afd08d5d3b10b89e11937be4_l3.png)
Multiply both sides by three and expand and simplify
![Rendered by QuickLaTeX.com \[3(PR)^2=\frac{x^2}{2}+\frac{y^2}{2}+\frac{z^2}{2}+2\sqrt{3}A\]](https://www.racquelsanderson.com/wp-content/ql-cache/quicklatex.com-08d35dcf1e79e5fda1cd6289af5df4d4_l3.png)
Hence, PQ=PR=RQ and triangle PQR is equilateral.
![]()
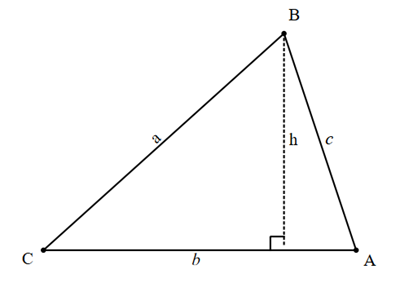
![]() in two ways.
in two ways.![]()
![]() or
or ![]()
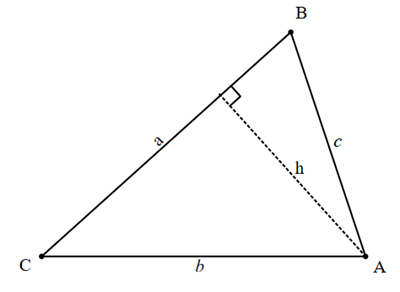
![]()
![]()
![]() therefore
therefore![]() or
or ![]()