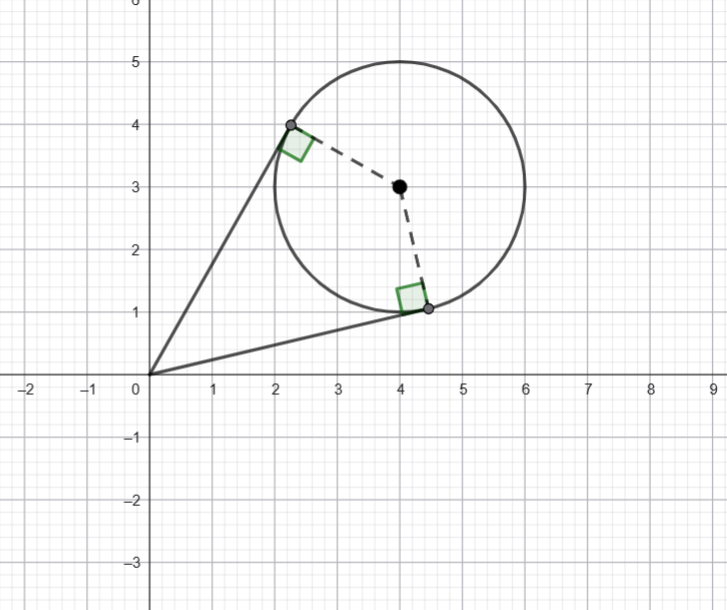
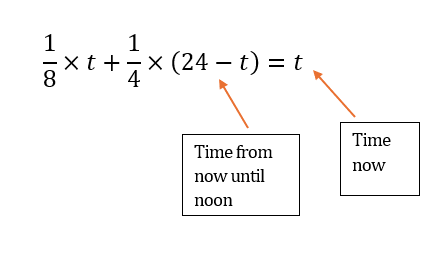
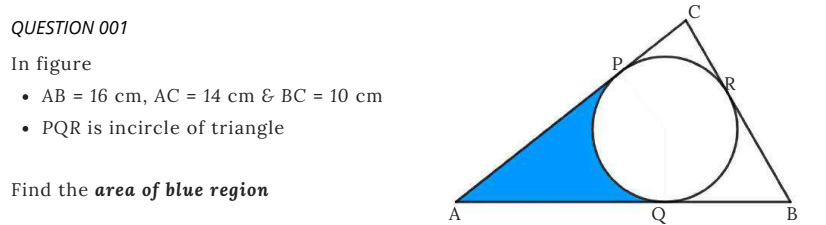
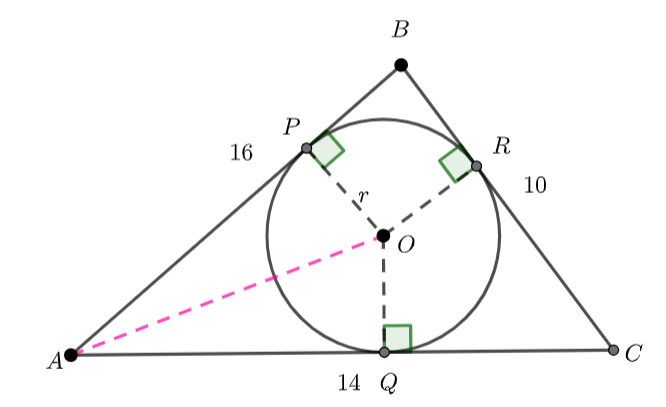
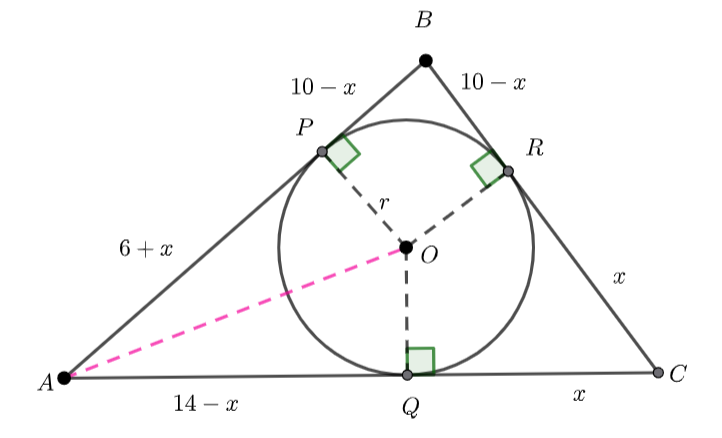
My Year 12 Specialist students are working on complex loci again. The following type of question always creates confusion.
| Let (a) Show that the locus of points satisfying (b) Find the centre and radius of the circle, expressing your answers in exact form. |
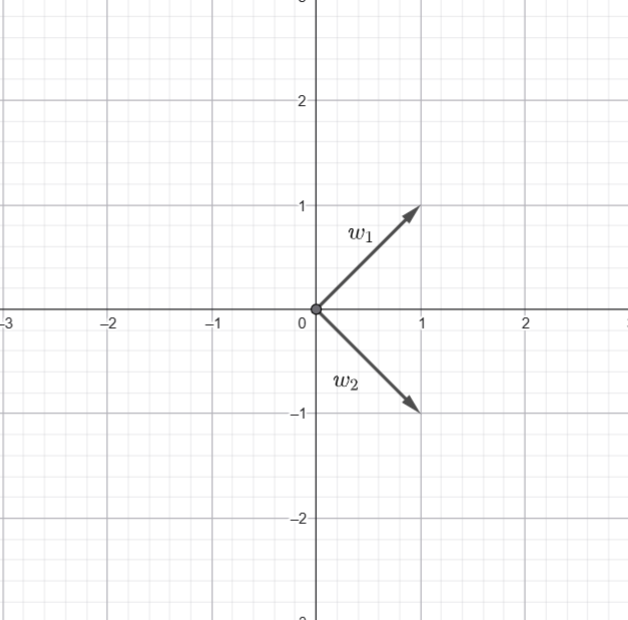
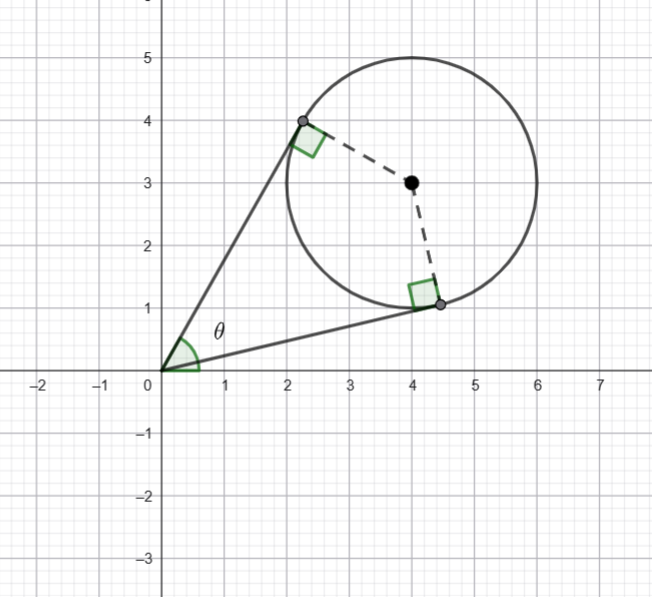
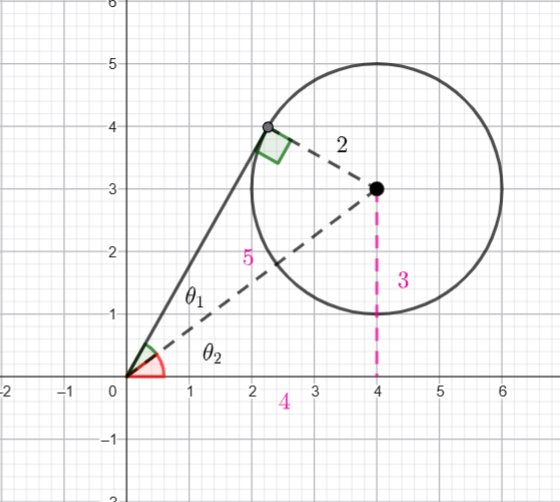
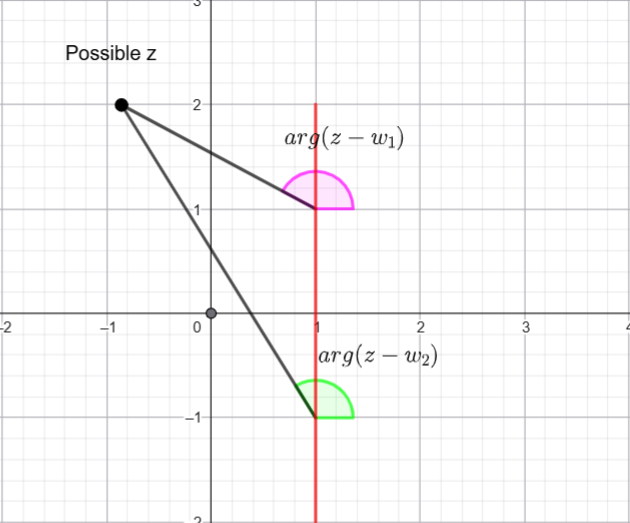
![]() is the angle the vector from
is the angle the vector from ![]() to
to ![]() makes with the positive
makes with the positive ![]() axis, likewise for
axis, likewise for ![]() .
.
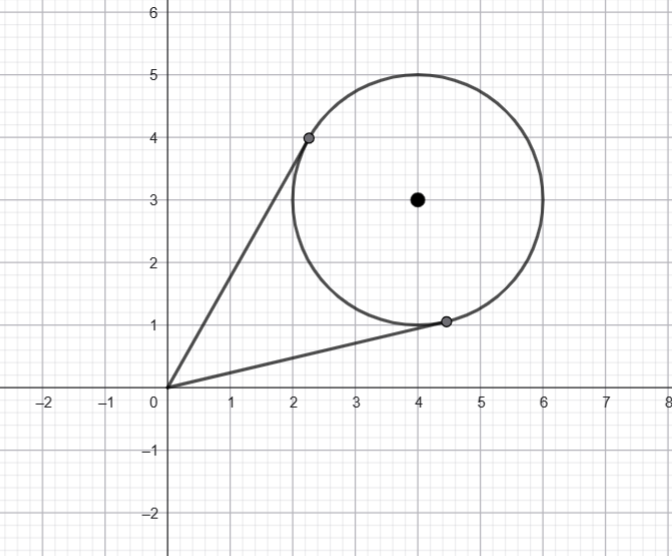
I am going to plot a possible ![]() and try to see the geometry that works.
and try to see the geometry that works.
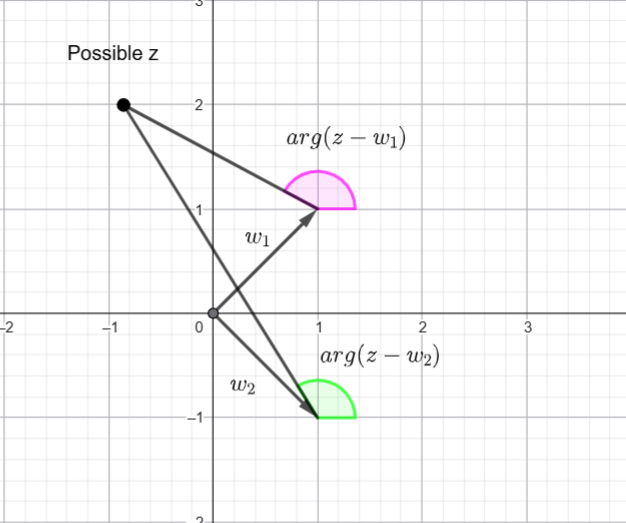
We want ![]()
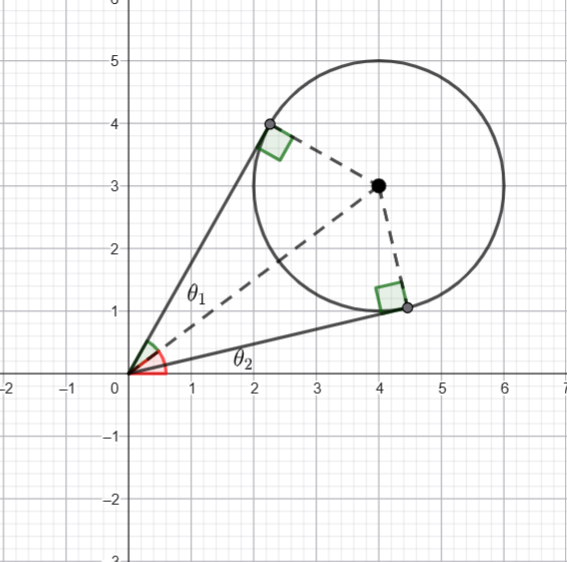
I am going to take advantage of some triangle geometry
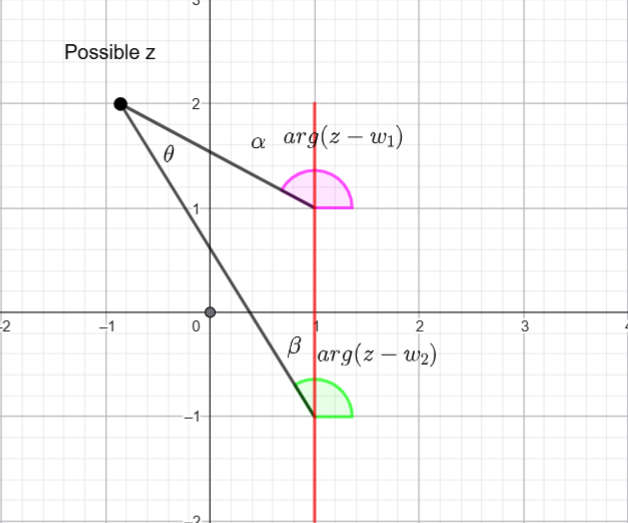
Using the External Angle Theorem, we know ![]()
![]()
Therefore ![]()
So we want all of the ![]() values that have an angle of
values that have an angle of ![]()
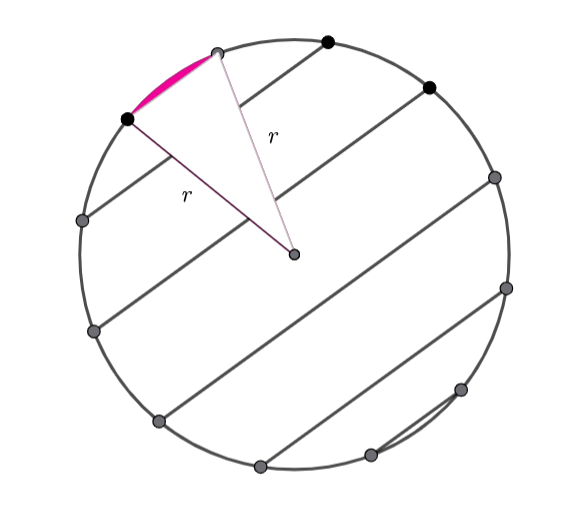
Now we are going to use some circle geometry -The angle at the circumference subtended by the same arc are congruent. So we need to find a circle that has those three points (![]() and
and ![]() ) on the circumference.
) on the circumference.
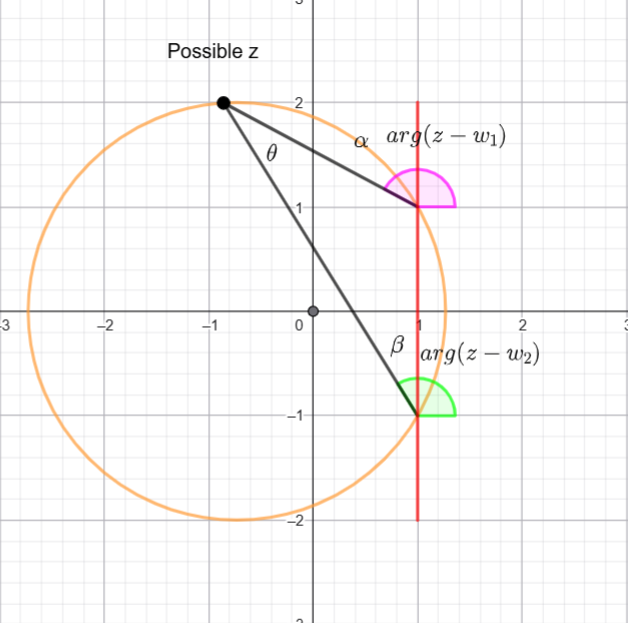
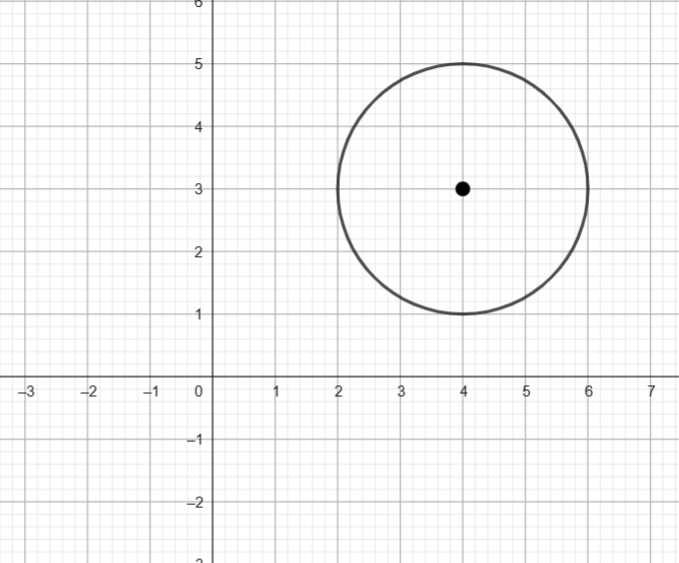
Hence the locus is

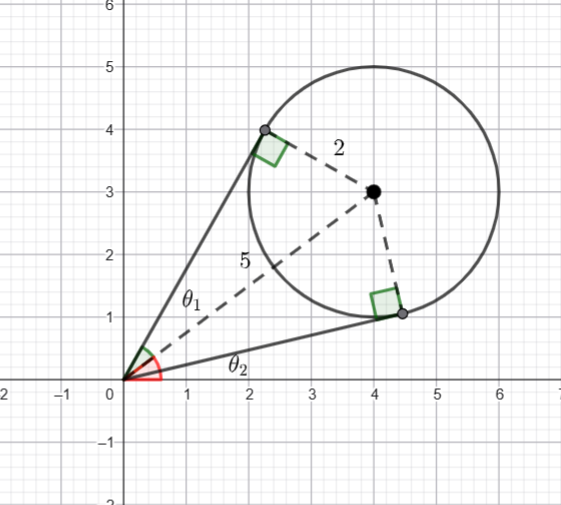
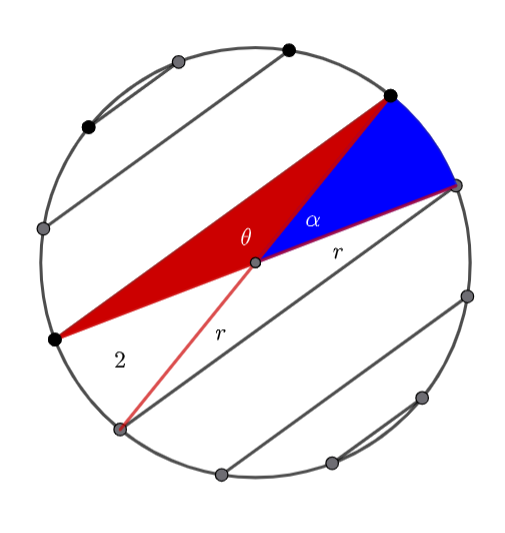
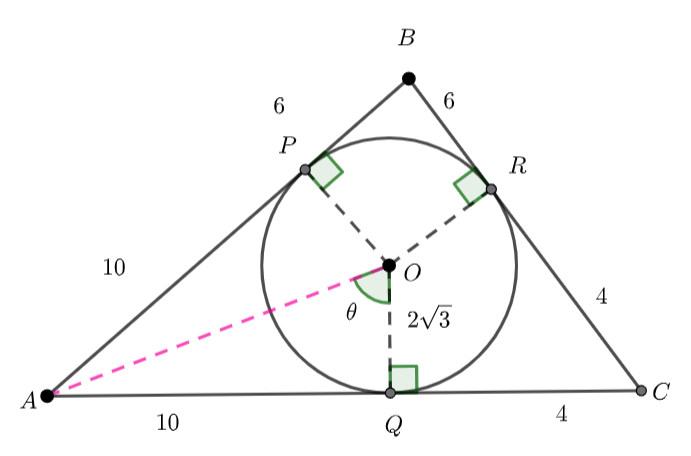
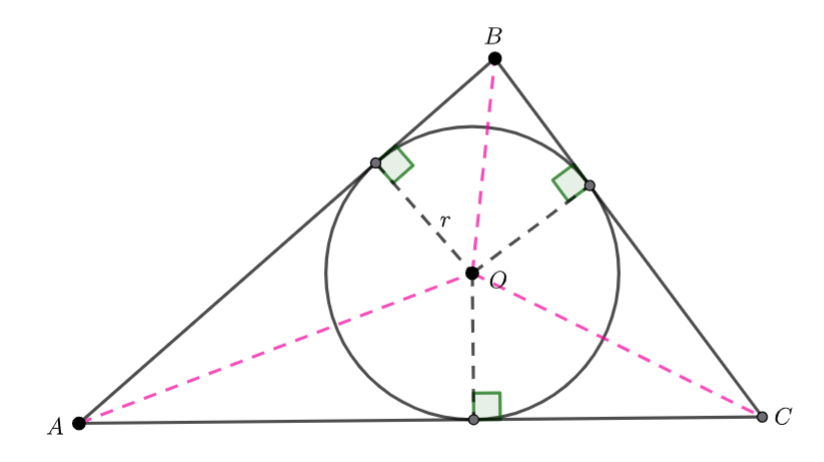
Now we need to find the radius and centre of the circle.
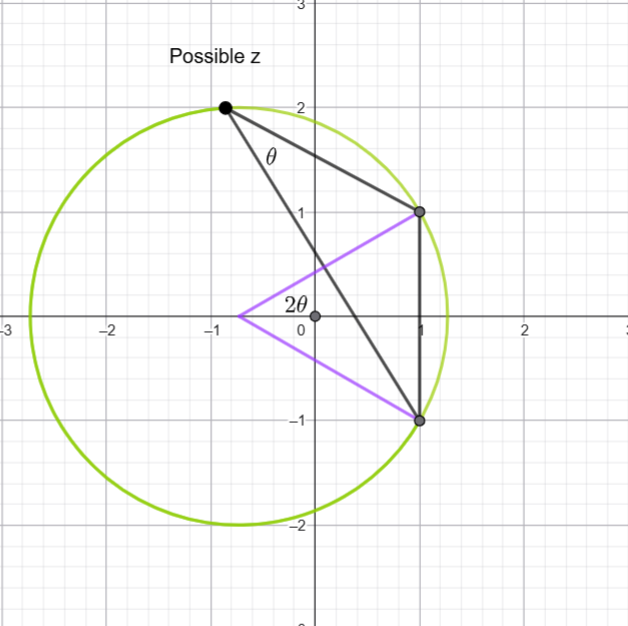
Using another circle theorem, the angle at the centre is twice the angle at the circumference.

The triangle must be equilateral (it is isosceles with a vertex angle of ![]() )
)
Hence the radius is 2.

![]()
Hence the centre is ![]()